Lista de referencia del menú
The menu, shown on the left, contains a complete list of buttons and commands, which are grouped into sections. Each section can contain two types of items, in this order:
Mathematical symbols, usually with little placeholder boxes.
Plain words: These are mathematical functions or programming commands, which usually require parameters. For example, think of
sin(angle)orrank(matrix).
Below are brief descriptions of the Menu sections. Note that some buttons are repeated if they belong to more than one category.
Símbolos
Aquí hay los símbolos matemáticos más comunes.
Nota
These buttons are for the nice-looking versions of the symbols. Sometimes you can write directly with the keyboard; it won't be charming, but it will work. For example, you can use the keyboard slash / for fractions. You can use the keyboard parentheses (), but the parentheses from buttons are better because they expand with the content.
Constantes
Constantes | ||
|---|---|---|
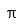 | Número pi | |
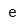 | Número e | |
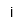 | Unidad imaginaria | |
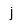 | Unidad imaginaria | |
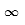 | Infinito | |
Se debe usar el botón para e y i. Las e y i del teclado son simples variables; no son las constantes.
Las cuatro operaciones básicas
Operaciones básicas | ||
|---|---|---|
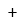 | Suma | |
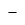 | Resta | |
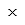 | ||
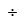 | División | |
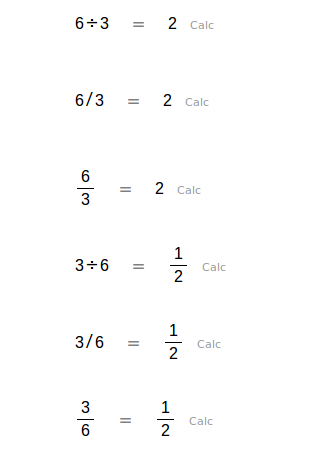
Se pueden usar varios signos para la multiplicación: asterisco *, punto medio ·, el botón del menú, y también un espacio space. Esto es, un espacio entre variables o números es realmente una multiplicación implícita. El asterisco * se convierte automáticamente al punto medio ·, que es más bonito.
Paréntesis
Paréntesis | ||
|---|---|---|
 | Paréntesis | |
 | Vector | |
 | Lista | |
 | Valor absoluto | |
 | Norma | |
No usar las llaves o los corchetes como paréntesis. Usar solamente los paréntesis.
[en] Expression | [en] Result |
|---|---|
: error | [en] Error |
: ok | [en] OK |
Símbolos bidimensionales
Símbolos bidimensionales | ||
|---|---|---|
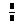 | Fracción | |
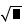 | Raíz cuadrada | |
 | Raíz | |
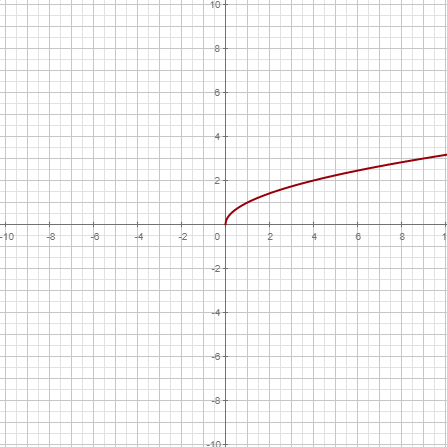
 | Potencia | |
 | Elemento de lista | |
Desigualdades
Desigualdades | ||
|---|---|---|
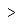 | Mayor que | |
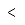 | Menor que | |
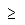 | Mayor o igual que | |
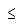 | Menor o igual que | |
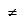 | Diferente de | |
Otros símbolos
Punto decimal
El punto . es para separar decimales, la coma , es para listas, y el apóstrofe '' ' '' es para derivar. El punto decimal es solamente el punto; los otros dos símbolos no tienen esa función.
Expression | Result | Expression | Result |
|---|---|---|---|
''3.1416'': OK | OK | ''.12'' | Error |
''3,1416'': Error | Error | ''0.12'' | OK |
''3'1416'': Error | Error | ''12.0'' | OK |
''1 234 567'': Error | Error | ''12.'' | OK |
You can convert an exact expression to approximate by making a simple operation with a decimal number, like multiplying by 1.0.
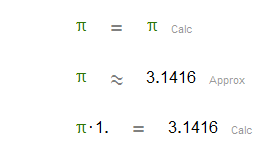 |
Más Menos
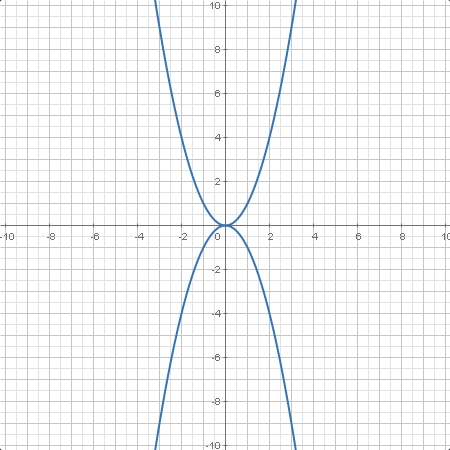
A veces estamos interesados en el resultado de una expresión cuando sumamos y restamos la misma cantidad, como cuando queremos calcular las raíces de un polinomio de grado dos. El símbolo nos permite eso y mucho más.
Si, por ejemplo, queremos calcular , esperamos
También podemos usarlo como un operador unario:
Cada signo posible se calculará cada vez que usemos el símbolo . Por tanto, si escribimos símbolos , obtendremos una lista con elementos. Algunos estarán repetidos ya que es una lista, no un conjunto (por ejemplo, ).
Podemos usar el símbolo en todas las operaciones básicas (suma, resta, producto, división, raíz, potencia) y algunas funciones elementales (exponencial, logaritmo, funciones trigonométricas e hiperbólicas y sus inversas).
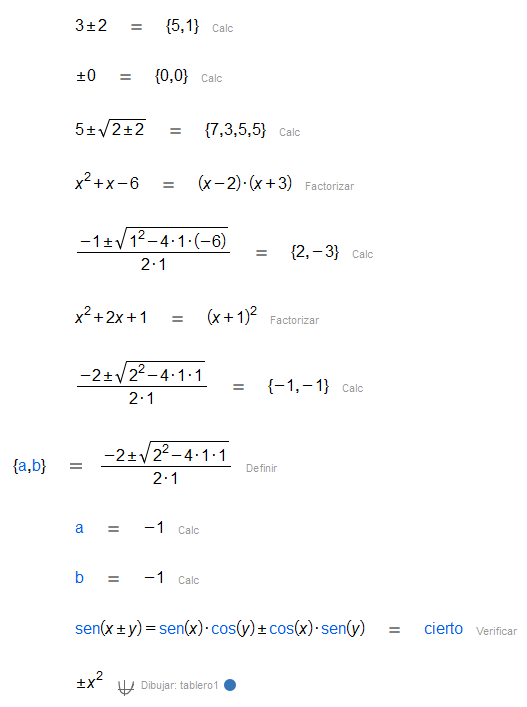 |  |
Ejemplos
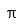 | |
|---|---|
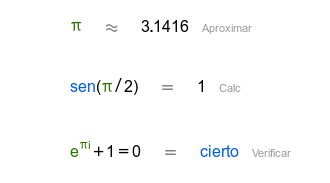 | |
 | |
 | |
 |  |
 | |
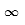 | |
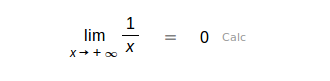 | |
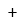 | |
 | |
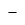 | |
 | |
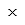 | |
 | |
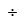 | |
 | |
 | |
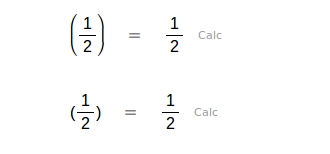 | |
 | |
 | |
 | |
 | |
 | |
 | 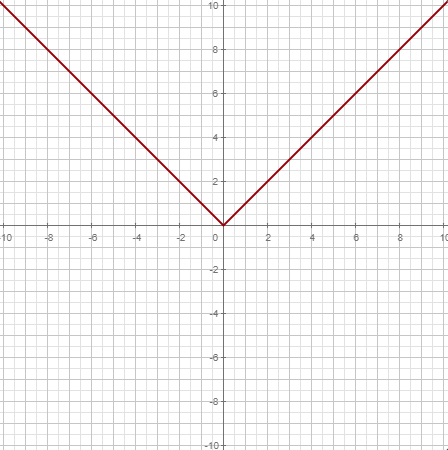 |
 | |
 | |
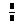 | |
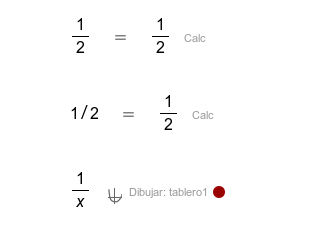 | 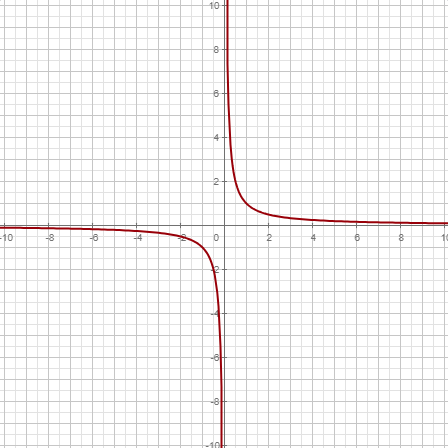 |
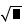 | |
 |  |
 | |
 | |
 | |
 |  |
 | |
 | |
 | |
 |  |
Aritmética
Aquí hay instrucciones acerca de números enteros y redondeo de decimales. También hay instrucciones sobre divisibilidad, que son comunes a los Polinomios.
Sugerencia
Puedes encontrar todos los comandos relacionados con la aritmética aquí.
Enteros y redondeo
Consultar también la sección de Configuración del documento para ver cuántos decimales se muestran.
Enteros y redondeo | |
|---|---|
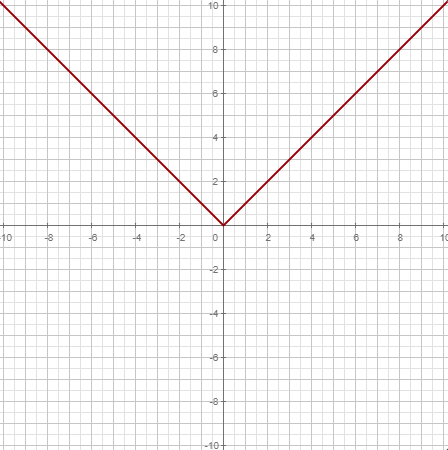
 | Valor absoluto |
 | Suelo |
 | Techo |
 | Redondea al entero más cercano, y para desempatar usa medio hacia arriba. |
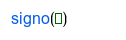 | El signo del número. Puede ser -1, 0 o 1. |
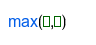 | El mayor de dos números, o de una lista. |
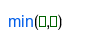 | El menor de dos números, o de una lista. |
 | Genera un número pseudo-aleatorio entre dos números dados (incluyendo ambos). También elige aleatóriamente de una lista. |
Divisibilidad
Divisibilidad | |
|---|---|
 | El numerador de una fracción. |
 | El denominador de una fracción. |
 | El cociente de la división entera entre el primer número (dividendo) y el segundo (divisor). |
 | El resto de la división entera entre el primer número (dividendo) y el segundo (divisor); también se llama |
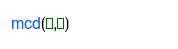 | Máximo común divisor |
 | Mínimo común múltiplo |
 | Descomposición de un entero en factores primos. |
 | Comprueba si un número es primo. Esto es un predicado: una instrucción que devuelve solamente |
Ejemplos
 | |
|---|---|
 |  |
 | |
 | |
 | |
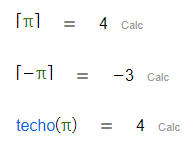 | |
 | |
 | |
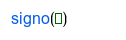 | |
 | |
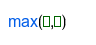 | |
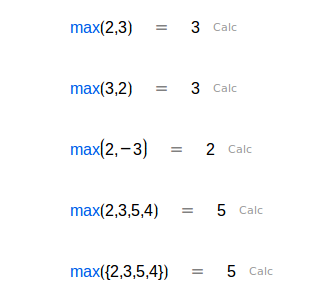 | |
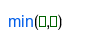 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
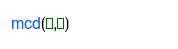 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
Polinomios
Los polinomios son funciones sencillas, pero son tan importantes que tienen su propia notación. Debido a que los polinomios se pueden dividir, comparten instrucciones de divisibilidad con la sección de Aritmética.
Sugerencia
Puedes encontrar todos los comandos disponibles relacionados con polinomios aquí.
Polinomios
Polinomios | |
|---|---|
 | Grado de un polinomio |
 | Cuantos términos tiene un polinomio |
 | Un término de un polinomio. El número de término se da en el segundo parámetro. Los términos están ordenados por grado descendente. Por ejemplo, el término número 1 es siempre el término principal. |
 | Contenido de un polinomio. Esto es, el mcd de sus coeficientes. |
 | Un polinomio de varias variables lo reordena alrededor de la variable dada en el segundo parámetro. |
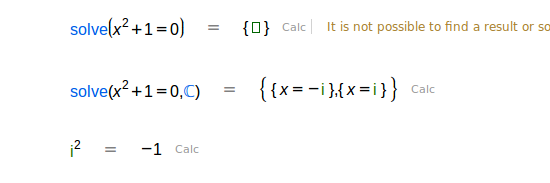
 | Encuentra las raíces de un polinomio, los valores de x que lo hacen 0. |
La instrucción
raíces(p)hace lo mismo queresolver(p=0)o aplicar la acciónCalcap=0, pero los resultados se muestran de manera distinta. Ver el ejemplo.También se pueden buscar raíces en los Complejos, si se usa como segundo parámetro el símbolo
Cde la sección Lógica y conjuntos. Ver el ejemplo.
Divisibilidad
Divisibilidad | |
|---|---|
 | Numerador de una fracción racional. |
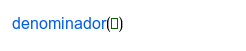 | Denominador de una fracción racional. |
 | Cociente de la división del primer polinomio (dividendo) entre el segundo (divisor). |
 | Resto de la división del primer polinomio (dividendo) entre el segundo (divisor). |
 | Mínimo común divisor. |
 | Máximo común múltiplo. |
 | Descomposición en polinomios irreductibles. |
 | Comprueba si un polinomio es irreductible. Esto es un predicado: una instrucción que devuelve solamente |
Números Complejos
Números Complejos | |
|---|---|
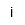 | Unidad imaginaria |
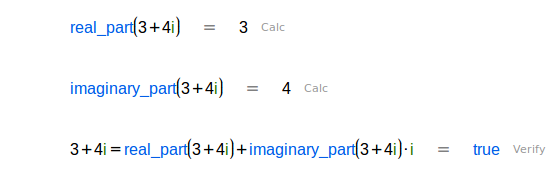
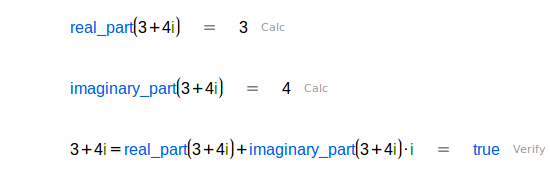
 | Parte real de un número complejo. |
 | Parte imaginaria de un número complejo, que es un número real. |
 | Módulo de un número complejo. |
 | Argumento de un número complejo, en el rango (-π,+π]. |
 | Convierte un número complejo de forma binomial a forma polar, y viceversa (!). La forma polar es una lista {norma, argumento}. |
 | Conjugado de un número complejo. Cambia el signo de la parte imaginaria. |
Ejemplos
 |
|---|
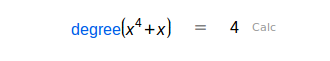 |
 |
 |
 |
 |
 |
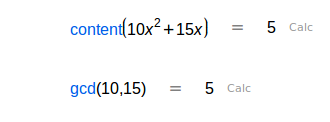 |
 |
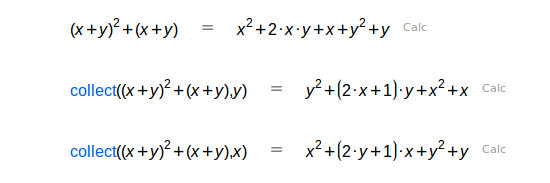 |
 |
 |
 |
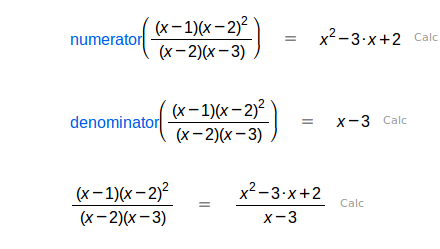 |
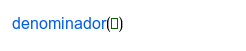 |
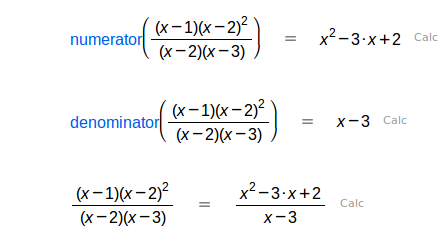 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
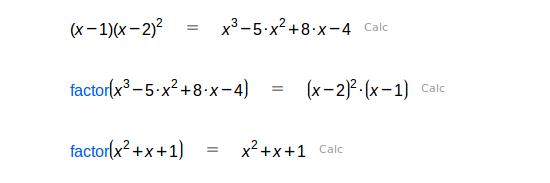 |
 |
 |
Números complejos |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
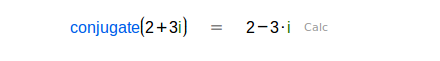 |
Estadística
Sugerencia
Puedes encontrar todos los comandos disponibles relacionados con el mundo de la estadística aquí.
Conjuntos de datos
Los conjuntos de datos (muestras) deben entrarse en forma de lista separada por comas, dentro de llaves {}.
Conjuntos de datos | |
|---|---|
 | Lista |
Un solo conjunto
Estas instrucciones resumen un conjunto de datos. De alguna manera, son capaces de medir su centro y su dispersión. Como hay varias definiciones de esto, también hay varias maneras de calcularlo, varias medidas estadísticas.
Descripción de un solo conjunto | |
|---|---|
 | Media, media aritmética, promedio |
 | Esto se usa para resumir medidas de unidades diferentes (longitud, coste, peso,...) de un mismo objeto. No tiene sentido por si solo, es útil solamente para hacer comparaciones de varios objetos. |
 | Esto es útil para razones, proporciones, cocientes... como por ejemplo velocidades. |
 | Medida de dispersión que es muy conveniente para hacer cálculos. |
 | Medida de dispersión que está en las mismas unidades que los datos. |
 | Medida de centralización, alternativa a la media, pero más robusta, porque no le afectan los valores extremos conocidos como outliers. |
 | Estos son valores que dividen los datos ordenados entre cuatro grupos del mismo tamaño. Se usan para resumir la dispersión. Ver la sección de formula reference. |
 | Valor más frecuente entre los datos. Puede ser un conjunto, si hay empates. |
Dos conjuntos
Estas instrucciones miden la relación entre datos apareados.
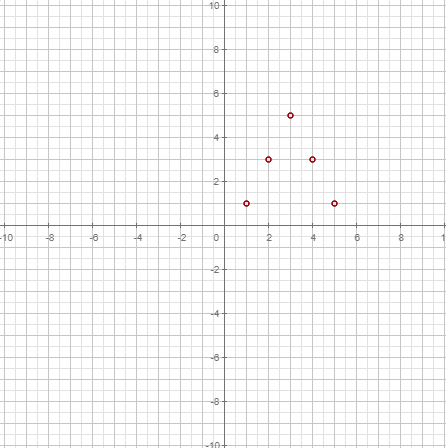
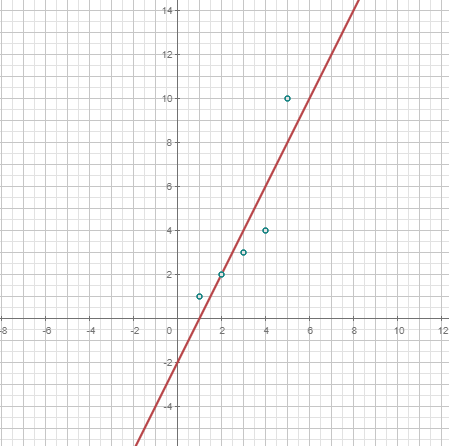
El conjunto de datos debe ser una lista de pares. La lista debe estar dentro de llaves
{}. Los pares deben ser con paréntesis(). Un lista con esta forma se usa para calcular, pero también se puede dibujar.
Relación entre dos conjuntos de datos apareados | |
|---|---|
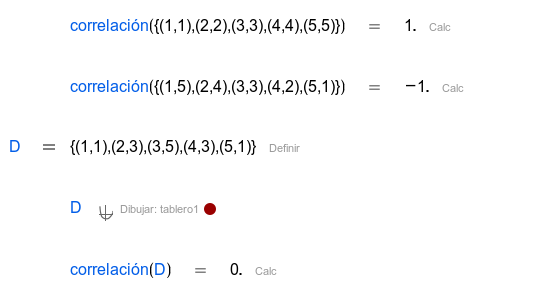
 | Esto es la base para el coeficiente de correlación. Tiene el mismo signo, pero su valor puede variar mucho. |
 | Coeficiente de correlación de Pearson. Determina si hay relación lineal entre los datos aparejados. |
 | Da la equación de la recta que mejor resume la nube de datos. |
 | Ajusta los datos a una potencia. |
 | Ajusta los datos a una función exponencial. |
 | Ajusta los datos a una función logarítmica. |
Referencia de fórmulas
Referencia de fórmulas | |
|---|---|
 | |
 | |
 | |
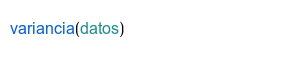 | |
 | |
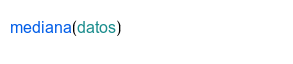 | |
 | |
 | |
 | |
 | |
Distribuciones de probabilidad
También es posible usar las distribuciones de probabilidad más comunes. Actualmente, están disponibles las siguientes
Distribuciones de probabilidad | |
|---|---|
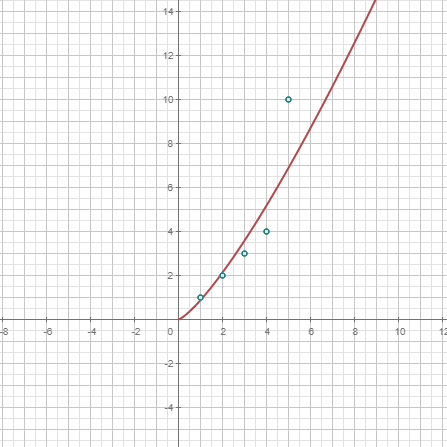
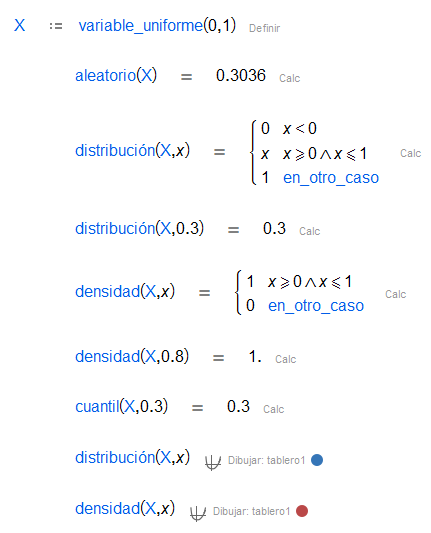
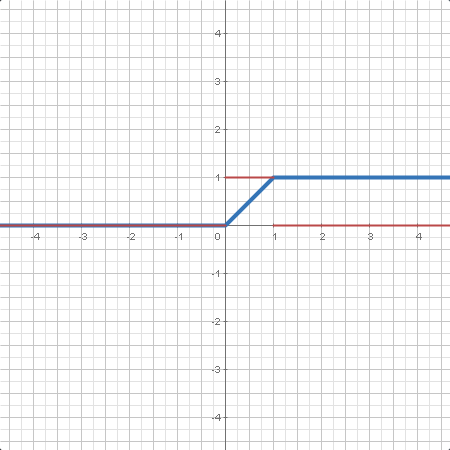
 | En la distribución uniforme, todos los intervalos de la misma longitud en el soporte de la distribución son equiprobables. |
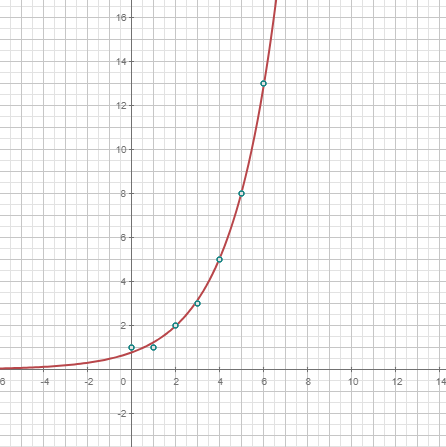
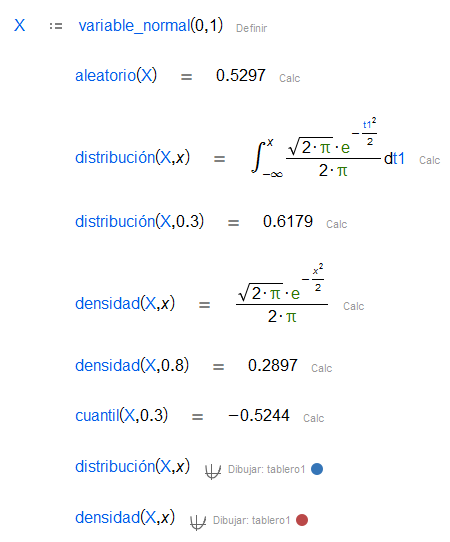
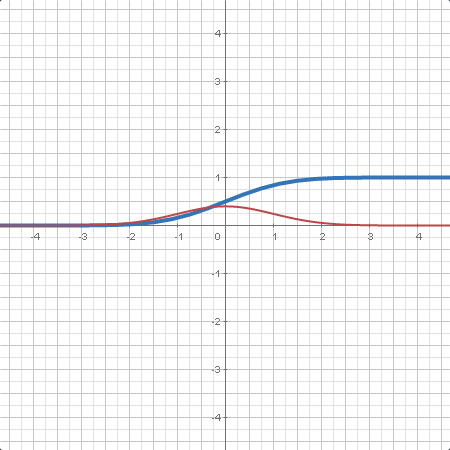
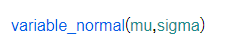 | La distribución normal está determinada por su media y su desvación estándar . Es muy usada en las ciencias naturales entre otros campos. |
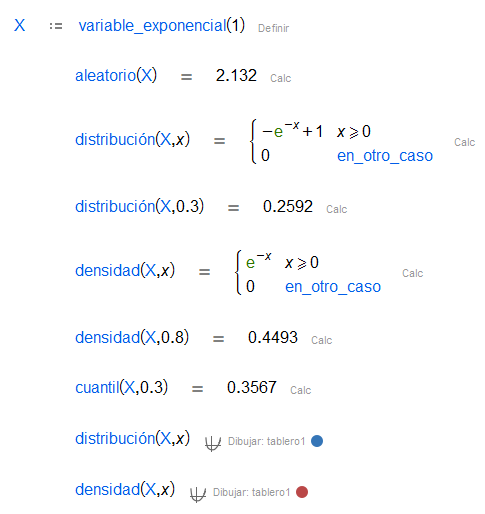
 | La distribución exponencial es la distribución de probabilidad que describe el tiempo entre eventos en un proceso de Poisson, es decir, un proceso donde los eventos ocurren de forma continuada e independiente en una ratio constante. |
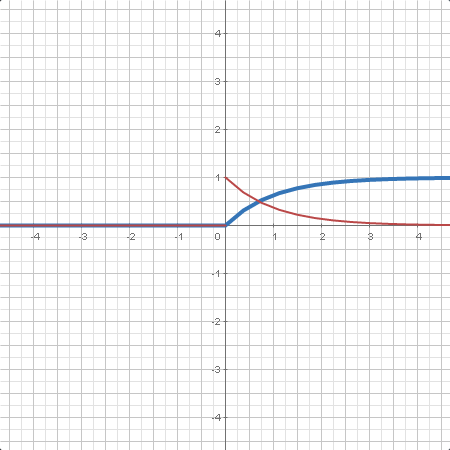
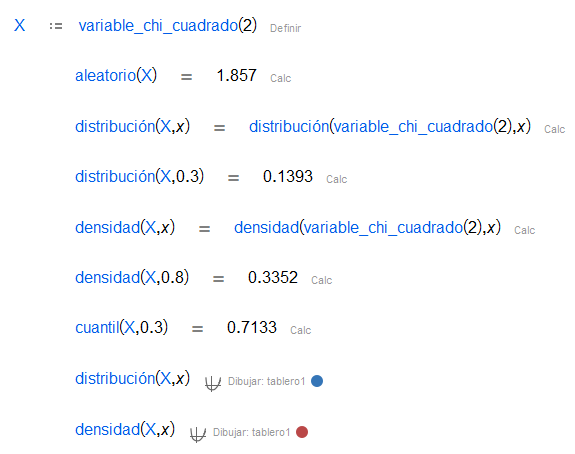
 | La distribución con grados de libertad es la distribución de la suma de los cuadrados de variables normales estándar independientes. |
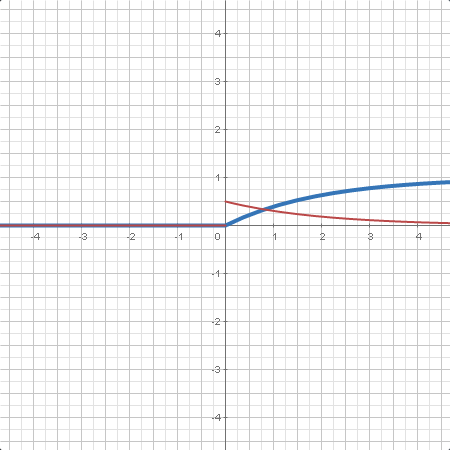
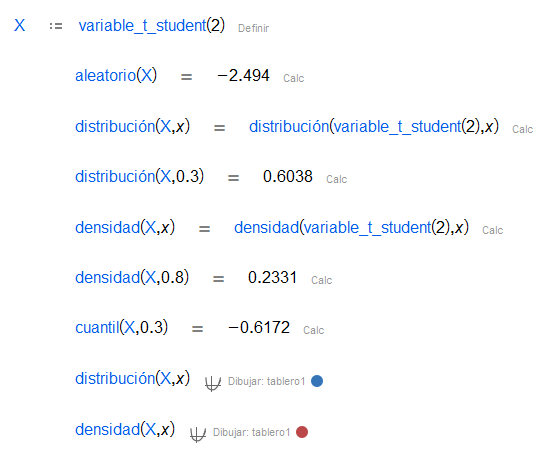
 | La distribución de Student aparece cuando se estima la media de una población reglada por una distribución normal en situaciones cuando el tamaño de la muestra es pequeño y la desviación estándar es desconocida. |
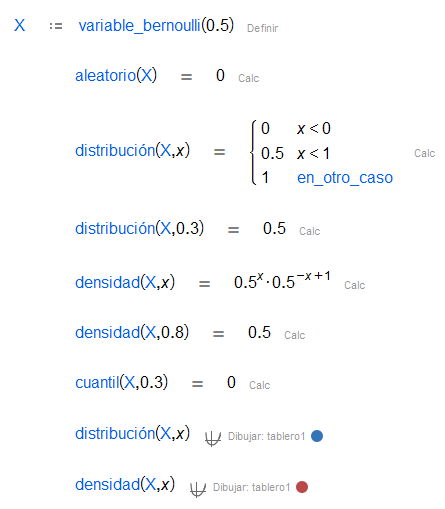
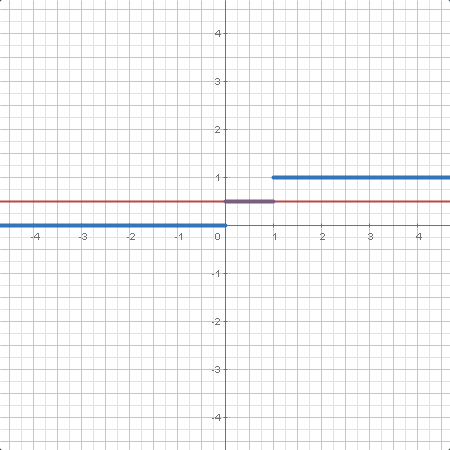
 | La distribución de Bernoulli es la distribución de probabilidad de una variable aleatoria que toma el valor con probabilidad y el valor 0 con probabilidad . |
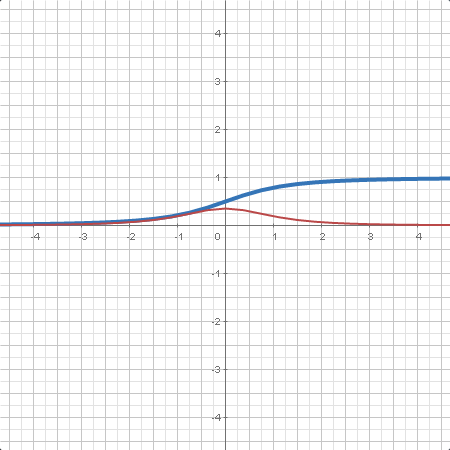
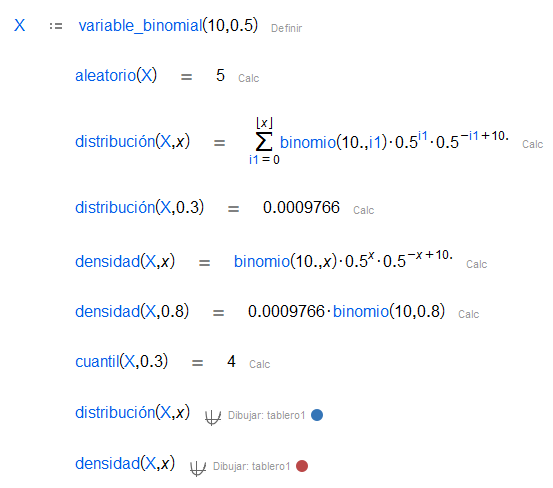
 | La distribución binomial con parámetros y es la distribución de probabilidad discreta del número de aciertos en una secuencia de experimentos independientes, cada uno siguiendo la misma distribución de Bernoulli. |
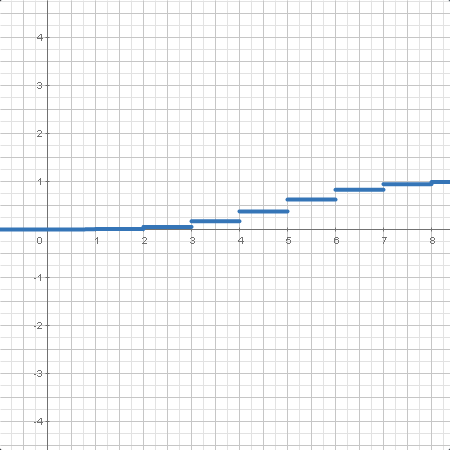
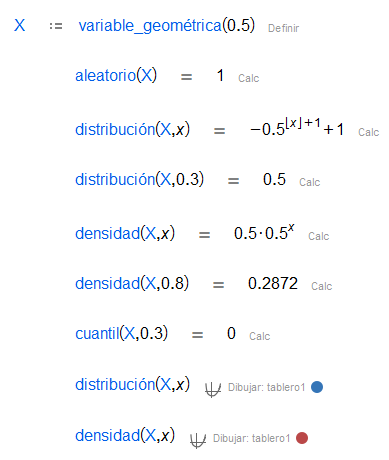
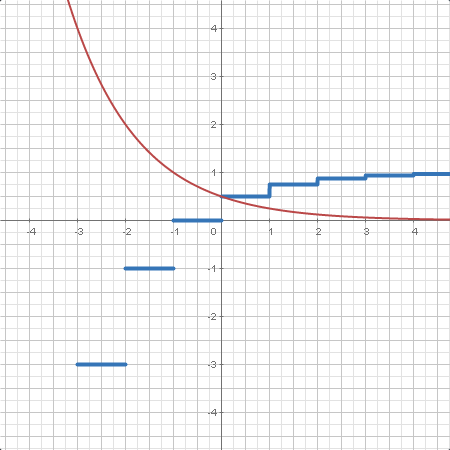
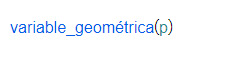 | La distribución geométrica con parámetro es la distribución de probabilidad discreta del número de fallos antes del primer acierto, cada intento siguiendo una variable de Bernoulli de parámretro . |
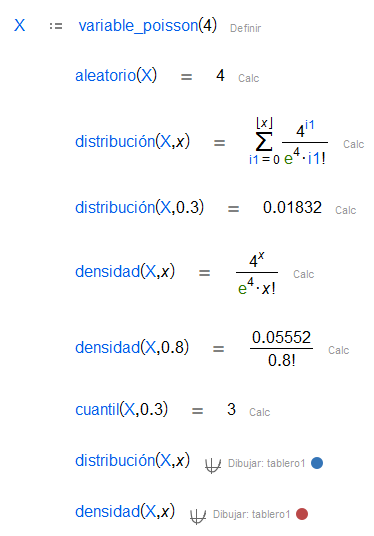
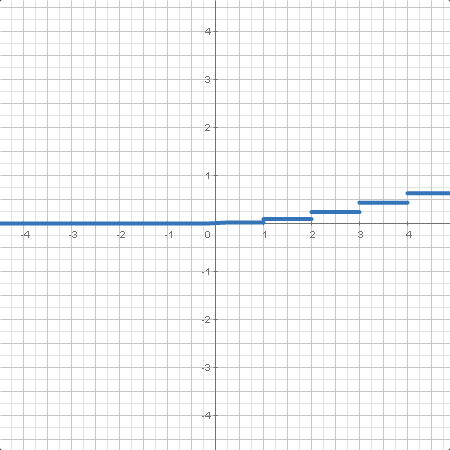
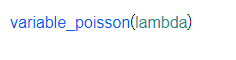 | La distribución de Poisson es una distribución de probabilidad discreta que expresa la probabilidad que un número de eventos ocurra en un intervalo fijo de tiempo o espacio si cada uno de estos eventos ocurre con una ratio constante e independiente del tiempo transcurrido desde el último evento. |
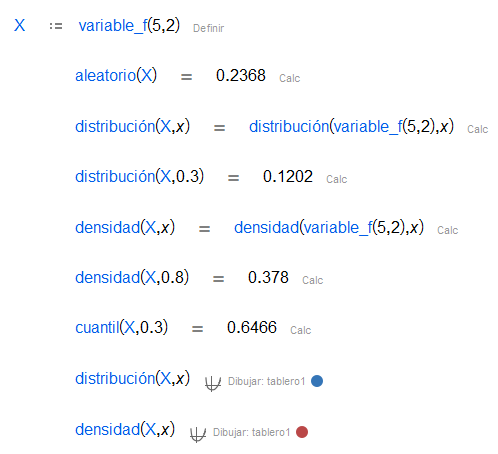
 | La distribución de es una distribución de probabilidad continua que aparece frecuentemente como la distribución nula de un test estadístico, más notablemente en el análisis de la varianza (ANOVA), e.g., test, . |
Además, se puede obtener un número aleatorio siguiendo tales distribuciones, obtener la función de distribución y densidad y encontrar el cuantil de una probabilidad dada.
Moreover, we can get a random number following such distributions, obtain its distribution and density function and find the quantile of given probability.
Funciones de probabilidad | |
|---|---|
 | Obtiene un número aleatorio siguiendo una distribución dada. |
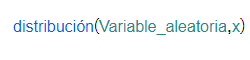 | Función de distribución de una variable aleatoria en un punto dado. En algunos casos, se da la expresión analítica. , función de distribución acumulada (CDF). |
 | Función de densidad de una variable aleatoria en un punto dando. En algunos casos, se da la expresión analítica. , función de densidad de probabilidad (PDF). |
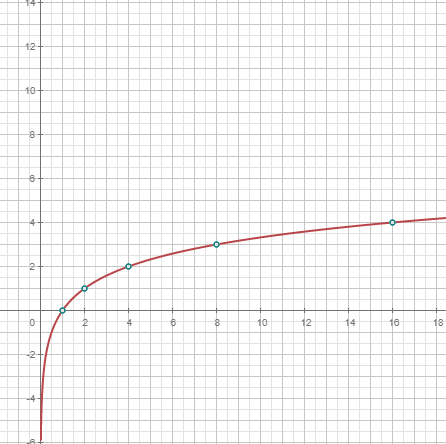
 | Función cuantil de una variable aleatoria dada una probabilidad. , función inversa de CDF. |
Representación de datos estadísticos
Statistical data representation | |
|---|---|
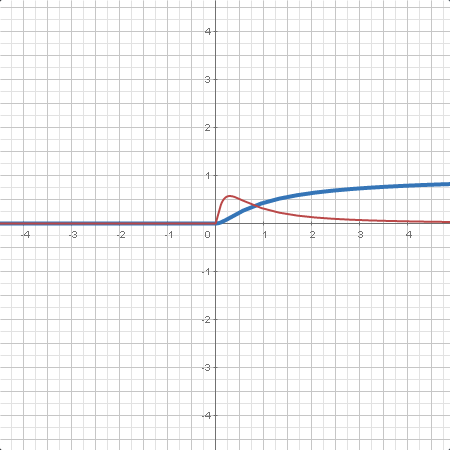
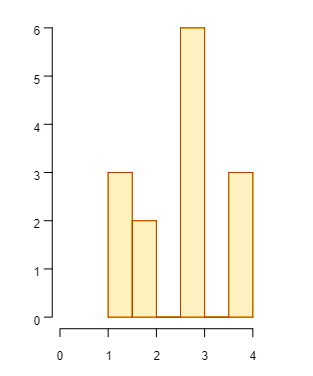
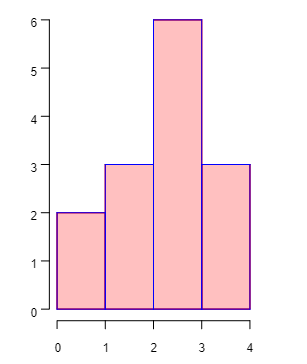
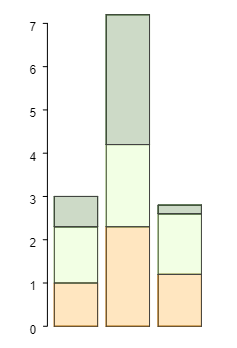
 | Los histogramas se utilizan para representar datos continuas de forma visual. |
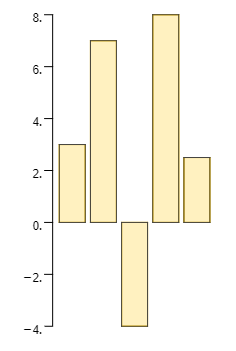
 | A diferencia de los histogramas, los diagramas de barras se utilizan para mostrar datos discretos o categóricos. |
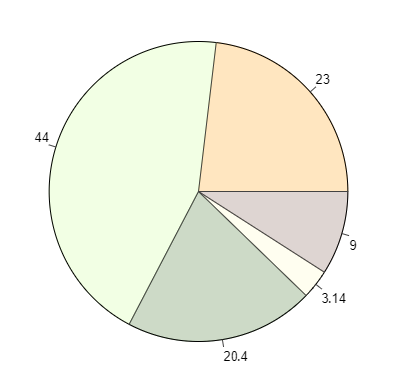
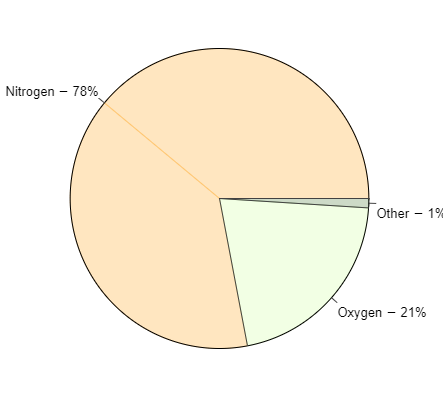
 | Los diagramas de sectores son otra herramienta común para datos categóricos, especialmente para mostrar la fracción del total que ocupa cada categoría. |
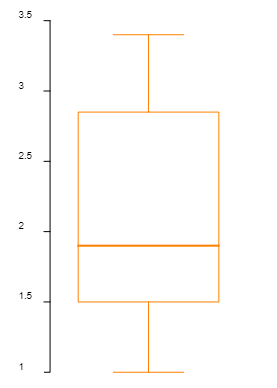
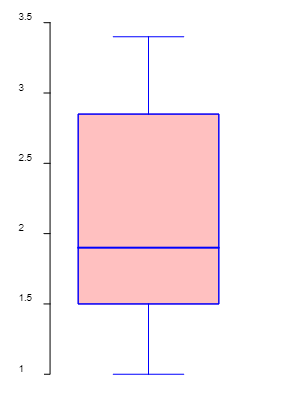
 | Las gráficas de cajas son muy útiles para representar conjuntos de datos de forma concisa. En una sola gráfica se ven la mediana, rango intercuartílico (IQR), y valores atípicos. |
Ejemplos
 | |
|---|---|
 | |
 | |
 | |
 | |
 | |
 | |
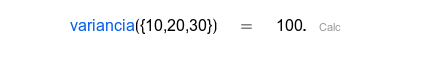 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 |  |
 | |
 |  |
 | |
 |  |
 | |
 |  |
 | |
 |  |
 | |
 |  |
 | |
 |  |
 | |
 |  |
 | |
 |  |
 | |
 |  |
 | |
 |  |
 | |
 |  |
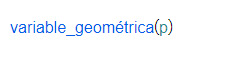 | |
 |  |
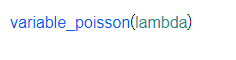 | |
 |  |
 | |
 |  |
 | |
 | |
 |  |
 | |
 | |
 |  |
 | |
 | |
 |  |
 | |
 | |
 |  |
Funciones
Las funciones más comunes son los polinomios y las funciones racionales; ambas son funciones algebraicas. Se explican en otra sección, Polynomials. Esta sección trata de otros grupos de funciones, llamadas funciones trascendentes. Sus valores exactos no se pueden calcular con aritmética básica. Se pueden calcular aproximaciones, pero no es práctico hacerlo manualmente. Es mejor usar una calculadora; antiguamente se usaba una tabla o libro entero de valores.
Sugerencia
Puedes encontrar todas los comandos disponibles relacionados con dichas funciones aquí.
Funciones trigonométricas
Las funciones trigonométricas provienen de la Geometría de los triángulos, pero ahora forman parte esencial de otros campos como Cálculo.
Funciones trigonométricas | ||
|---|---|---|
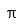 | Númeror pi. Es útil para trabajar en radianes. | |
 | Grado angular | |
Directas | ||
 | Seno, relacionado con el lado opuesto al ángulo. | |
 | Coseno, relacionado con el lado adyacente al ángulo | |
 | Tangente, sen/cos | |
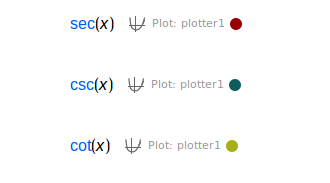
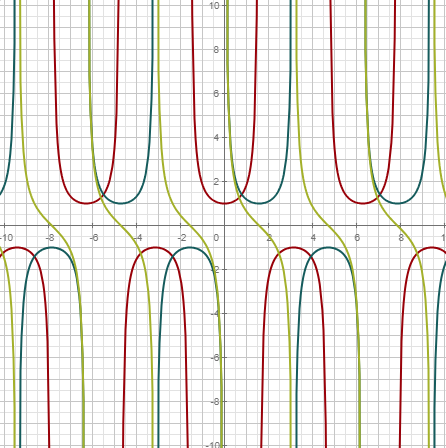
Recíprocas | ||
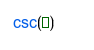 | Cosecante, 1/sen | |
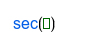 | Secante, 1/cos | |
 | Cotangente, 1/tan | |
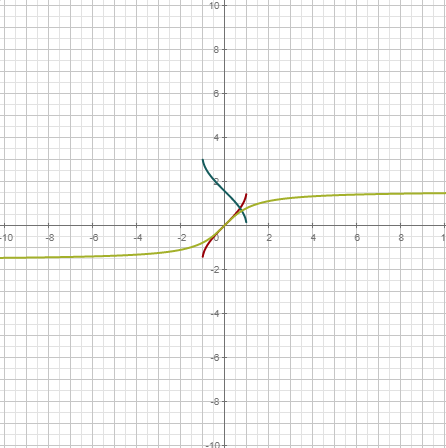
Inversas | ||
 | Devuelve uno de los varios ángulos cuyo seno es el número introducido. Estará en el intervalo [-π/2,π/2]. | |
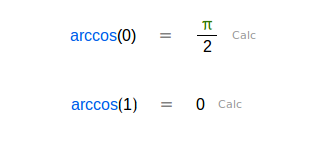
 | Devuelve uno de los varios ángulos cuyo coseno es el número introducido. Estará en el intervalo [0,π]. | |
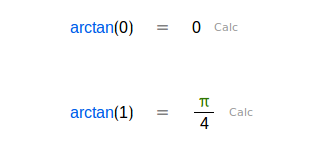
 | Devuelve uno de los varios ángulos cuya tangente es el número introducido. Estará en el intervalo (-π/2,π/2). | |
Se puede usar la acción Simplificar para forzar más simplificaciones en las expresiones trigonométricas. Además, la acción Verificar puede comprobar identidades trigonométricas.
You can use the Simplify action to force non-trivial simplifications over trigonometric expressions. Moreover, the Verify action can test for trigonometric identities.
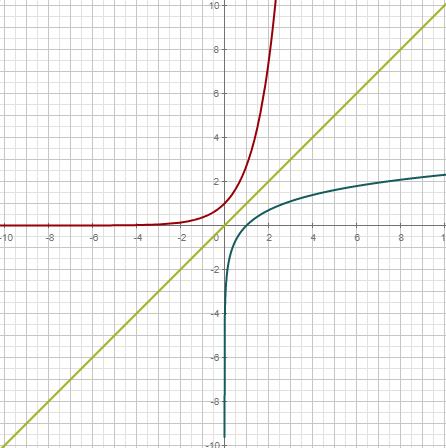
Logaritmos y exponenciales
Las funciones exponenciales y logarítmicas son muy importantes en Cálculo. Además, el logaritmo se usa en medidas físicas, como el pH en química y los dB en acústica.
Logaritmos y exponenciales | |
|---|---|
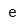 | Número e. Es la base del logaritmo neperiano. |
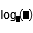 | Logaritmo con base |
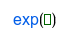 | Exponencial, |
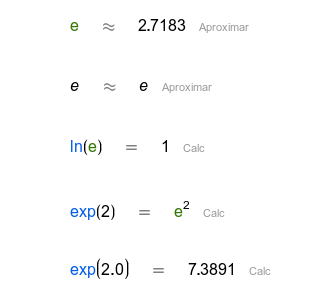
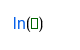 | Logaritmo neperiano o natural |
 | Logaritmo |
Se debe entrar e con el botón. No se puede simplemente teclear e con el teclado, porqué entonces es solamente una variable sin valor, no el número.
You must enter e with the button. You can't simply type e with the keyboard because then it's just a variable called e but not the number. The logarithm base can be set as a subindex of the function log(). If no base is set, just log() means the decimal logarithm or, in other words, the base 10 logarithm. Also, ln() means the natural logarithm, which is the base e logarithm.
Se puede usar la acción Simplify para forzar más simplificaciones en las expresiones logarítmicas o exponenciales. Además, la acción Verify puede comprobar identidades.
Funciones hiperbólicas
Funciones hiperbólicas | |
|---|---|
 | |
 | |
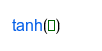 | |
Ejemplos
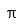 |  |
|---|---|
 | |
Funciones trigonométricas | |
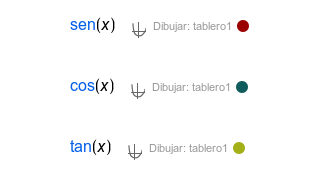 | 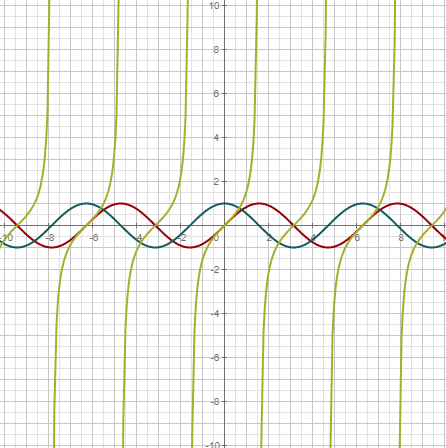 |
 | |
 | |
 | |
 | |
 | |
 | |
Funciones trigonométricas recíprocas | |
 |  |
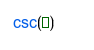 | |
 | |
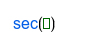 | |
 | |
 | |
 | |
Funciones trigonométricas inversas | |
 |  |
 | |
 | |
 | |
 | |
 | |
 | |
Funciones logarítmicas y exponenciales | |
 |  |
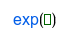 | |
 | |
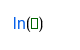 | |
 | |
 | |
 | |
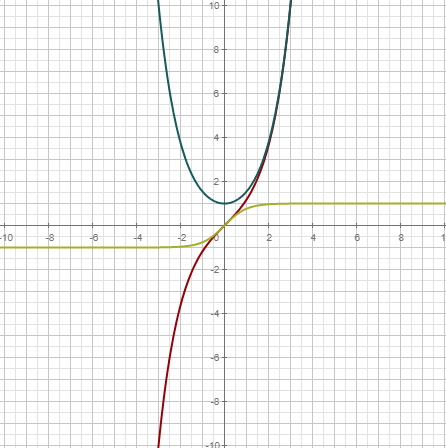
Funciones hiperbólicas | |
 |  |
 | |
 | |
 | |
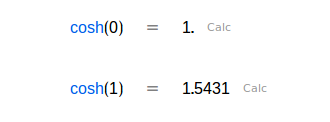 | |
 | |
 | |
Cálculo
Sugerencia
Puedes encontrar todos los comandos disponibles relacionados con cálculo aquí.
Aquí se agrupan un montón de botones importantes para cálculo, funciones y sucesiones.
Acciones | |
|---|---|
 | Derivar |
 | Integrar |
La derivada o la integral usan de forma predeterminada la primera variable en orden alfabético. Se puede cambiar esto configurando la acción, haciendo clic en el icono de la línea.
Botones | |
|---|---|
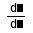 | Derivada. También se puede usar el apóstrofe (') del teclado. |
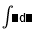 | Integral con diferencial |
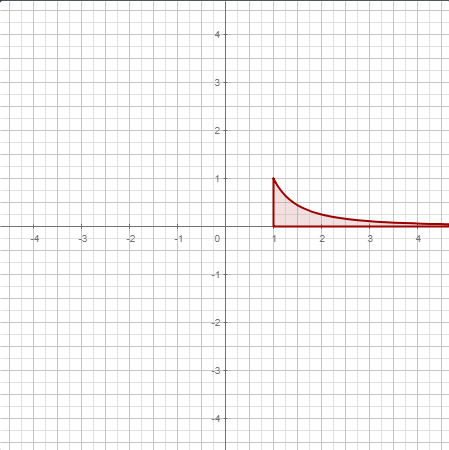
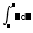 | Integral definida con diferencial. Tenga en cuenta que el signo de la función es importante. La integral definida no siempre es el área. |
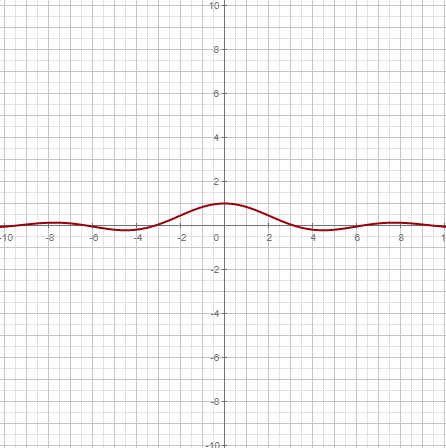
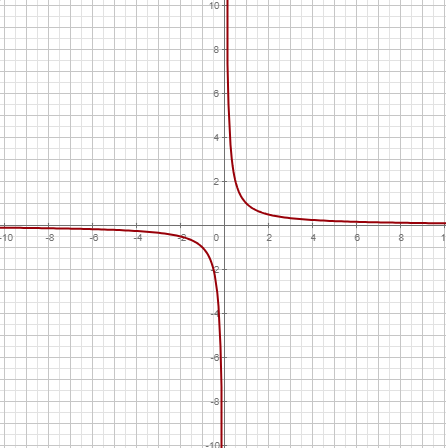
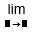 | Límite. Se puede usar |
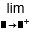 | Límite por la derecha |
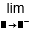 | Límite por la izquierda |
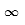 | Hasta el infinito... ¡y más allá! |
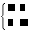 | Función definida a trozos |
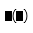 | Aplicación de función |
 | Expresión con un dominio restringido |
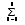 | Sumatorio con elementos abajo y encima |
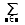 | Sumatorio con elemento abajo |
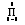 | Productorio con elementos abajo y encima |
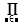 | Productorio con elemento abajo |
Aplicación de función debe usarse solamente cuando la función no está todavía definida, como en las EDOs. No usar para definir o evaluar una función; usar para eso paréntesis simples del teclado. Ver el ejemplo.
Instrucciones | |
|---|---|
 | Dominio de una función |
 | Polinomio de Taylor |
Ecuaciones Diferenciales Ordinarias | |
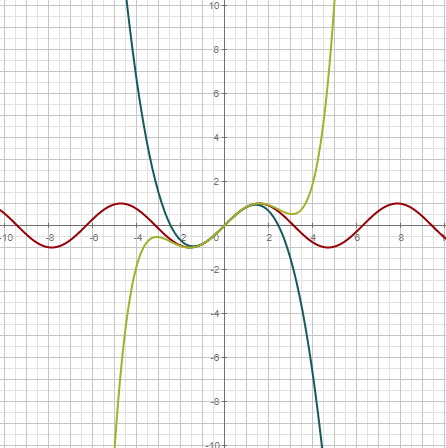
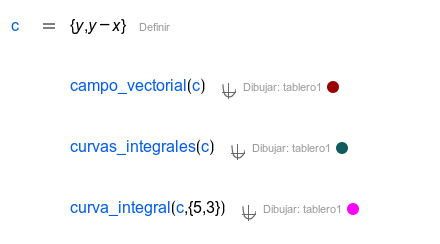
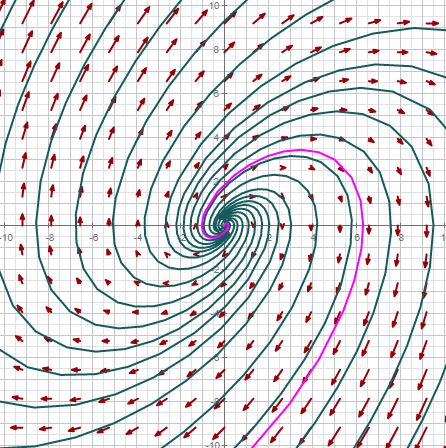
 | Rellena el plano con vectores definidos por la función. Usar para visualizar gradientes, fuerzas, derivadas en el espacio de fases,... |
 | Rellena el plano con curvas que siguen el campo vectorial dado; esto es, curvas que son soluciones de la EDO asociada al campo vectorial. Usar para obtener una vista general de la estabilidad del campo. |
 | Dibuja una única curva solución, que empieza en el punto dado. |
Ejemplos
 | 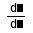 |
|---|---|
 | 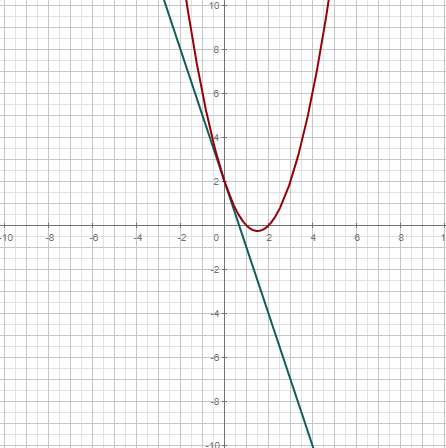 |
 | 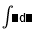 |
 | |
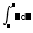 | |
 |  |
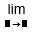 | |
 |  |
 |  |
 |  |
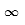 | |
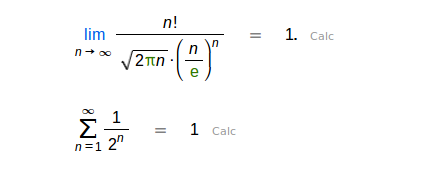 | |
 | |
 | 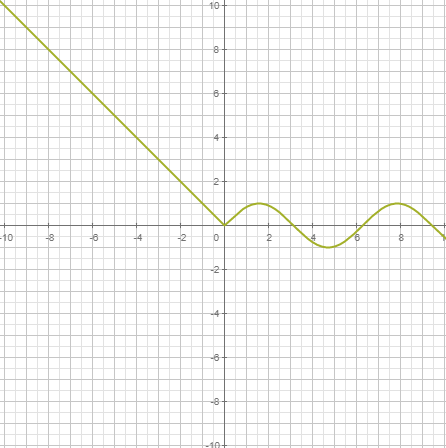 |
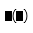 | |
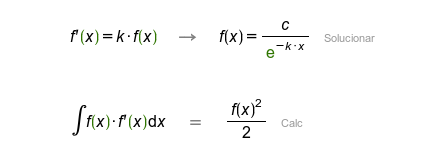 | |
 | |
 |  |
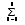 | 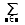 |
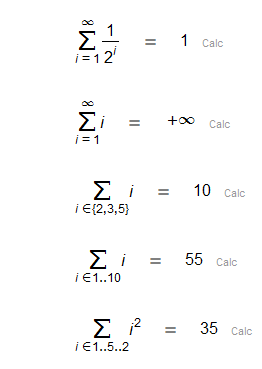 | |
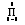 | 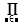 |
 | |
 | |
 | |
 | |
 |  |
   | |
 |  |
Álgebra lineal
Sugerencia
Puedes encontrar todos los comandos disponibles relacionados con álgebra lineal aquí.
Aquí se encuentran las operaciones de vectores y matrices. Los vectores usan corchetes y se escriben horizontalmente. Se pueden escribir con el botón del menú, o directamente con el teclado.
Las matrices se escriben mejor con el botón del menú. Sin embargo, también se pueden escribir con el teclado como un vector de vectores de dimensiones iguales, como en otros lenguajes de programación. Una vez la matriz ya está creada, todavía se puede modificar su estructura. Se puede, por ejemplo, insertar o eliminar columnas y filas. Hay botones para ello en el menú. Normalmente están desactivados, pero se activan cuando el cursor entra en una matriz.
Los vectores automáticamente se reconocen como matrices en algunas instrucciones. No es necesario preocuparse de hacer la conversión. Las operaciones habituales se adaptan a vectores y matrices. Por ejemplo, el símbolo de multiplicar significa cosas diferentes cuando se usa entre un escalar y un vector, dos vectores, un vector y una matriz, o dos matrices.
Álgebra lineal | |
|---|---|
Constructores | |
 | Vector |
 | Matriz |
 | Determinante |
Botones para vectores | |
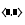 | Producto escalar |
 | Producto vectorial |
 | Norma |
 | Elemento de vector |
Botones para matrices | |
 | Determinante |
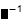 | Inversa |
 | Traspuesta |
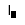 | Matriz identidad |
 | Elemento de matriz |
Instrucciones | |
 | Dimensión de un vector |
 | Dimensiones de una matriz: primero filas, después columnas. |
 | Rango de una matriz; máximo número de filas y columnas linealmente independientes. |
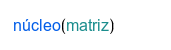 | Una matriz cuyas columnas son una base del núcleo. |
 | Una matriz cuyas columnas son una base de la imagen. |
 | Lista de valores propios, repetidos tantas veces como su multiplicidad. |
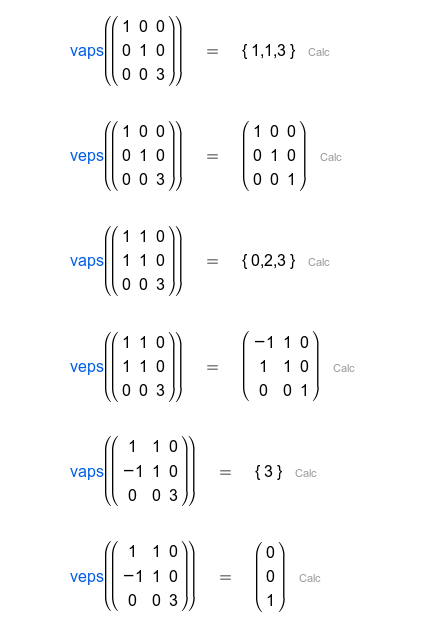
 | Una matriz cuyas filas son vectores propios, ordenadas igual que el resultado de la instrucción |
 | Forma normal de Jordan de la matriz, si existe. Da la forma triangular inferior, no la superior. |
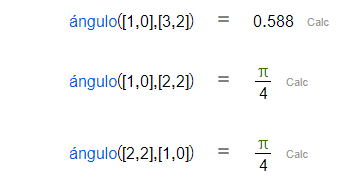
 | Ángulo entre dos vectores. |
En las instrucciones núcleo(), imagen() y veps(), el resultado es una matriz cuyas columnas son vectores que forman una base. Observe que, como hay muchas bases diferentes, puede haber muchos resultados diferentes. Se puede separa un vector en particular del resultado R usando RT1, RT2, RT3,...
For the kernel(), image() and eigenvectors() commands, the result is a matrix whose columns are the vectors that form a base. Note that, because there are always many bases, there are many other correct results. You can get a particular vector from the result R using RT1, RT2, RT3,...
Modificadores de estructura de matriz | |
|---|---|
 | Insertar columna a la izquierda |
 | Insertar columna a la derecha |
 | Eliminar columna |
 | Insertar fila encima |
 | Insertar fila debajo |
 | Eliminar fila |
Ejemplos
 |
|---|
 |
 |
 |
 |
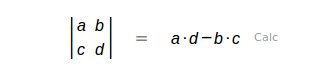 |
 |
 |
 |
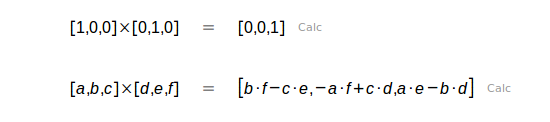 |
 |
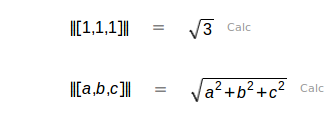 |
 |
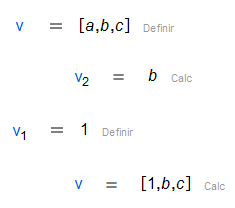 |
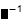 |
 |
 |
 |
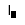 |
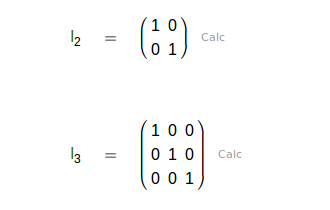 |
 |
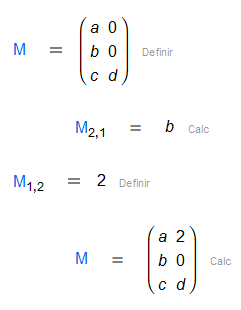 |
 |
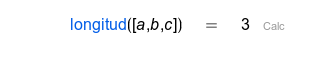 |
 |
 |
 |
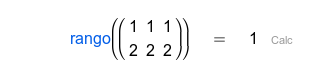 |
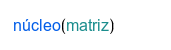 |
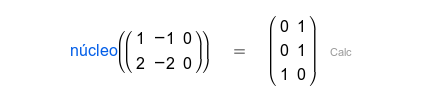 |
 |
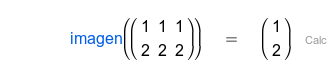 |
  |
 |
 |
 |
 |
 |
Combinatoria
Sugerencia
Puedes encontrar todos los comandos disponibles relacionados con la combinatoria aquí.
Aquí se encuentran las funciones combinatorias básicas. Se pueden calcular sus valores. También se pueden aplicar estas funciones a una lista para ver la colección entera. Por favor, tenga cuidado; los resultados fácilmente pueden ser muy grandes.
Combinatoria | |
|---|---|
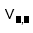 | Variaciones |
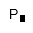 | Permutaciones |
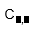 | Combinaciones |
 | Variaciones con repetición |
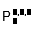 | Permutaciones con repetición |
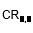 | Combinaciones con repetición |
 | Coeficiente binomial, número combinatorio. |
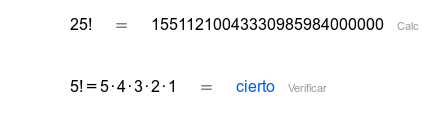
 | Factorial. También se puede escribir |
Ejemplo
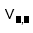 |
|---|
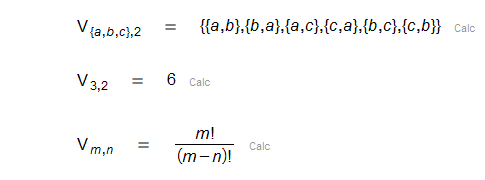 |
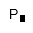 |
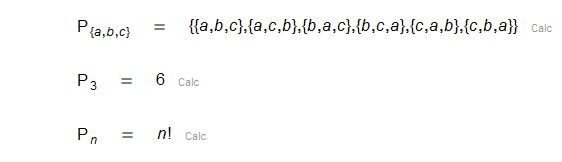 |
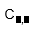 |
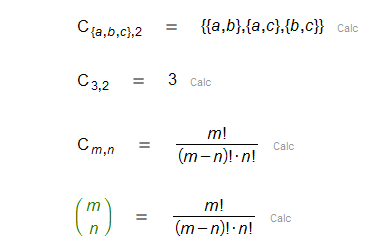 |
 |
 |
 |
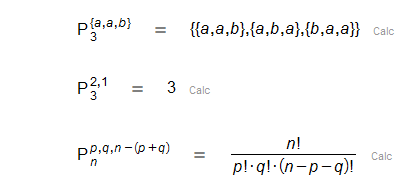 |
 |
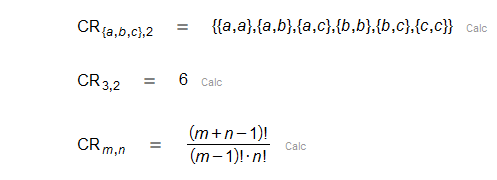 |
 |
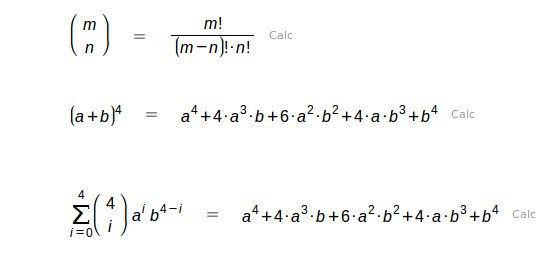 |
 |
 |
Lógica y conjuntos
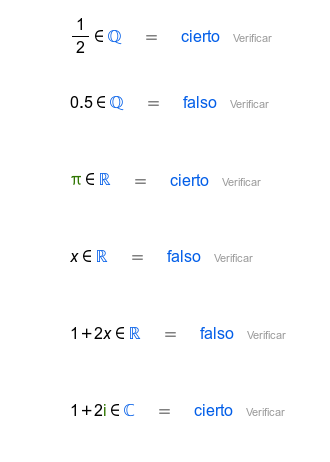
Se puede verificar si una afirmación es cierta o falsa. Se usa para comprobar identidades, por ejemplo. Hay operadores lógicos (Booleanos), que se pueden usar para combinar afirmaciones.
conjuntos finitos: una lista de elementos dentro de llaves, como
{1,2,3}.conjuntos notables de números: representados por símbolos, por ejemplo,
R.
Se pueden hacer operaciones con los conjuntos finitos, pero no con los otros. También puedes trabajar con intervalos y hacer operaciones con ellos.
Intervalos | |
|---|---|
 | El intervalo , es decir todos los números de entre y : |
 | El intervalo , es decir todos los números entre y incluyendo : |
 | El intervalo , es decir todos los números entre y incluyendo : |
 | El intervalo , es decir todos los números entre y incluyendo ambos y : |
The main operations you can perform are described below.
Lógica y conjuntos | |
|---|---|
Acciones | |
 | Verificar |
Botones de lógica | |
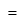 | Igual |
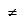 | No igual |
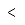 | Menor |
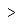 | Mayor |
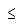 | Menor o igual |
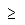 | Mayor o igual |
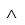 | Y lógico |
 | O lógico |
Botones de conjuntos | |
 | Lista |
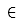 | Pertenece |
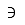 | Contiene |
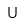 | Unión |
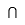 | Intersección |
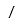 | Resta de conjuntos |
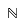 | Números naturales |
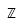 | Números enteros |
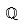 | Números racionales |
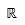 | Números reales |
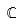 | Números complejos |
Ejemplos
 | |||||
|---|---|---|---|---|---|
 | |||||
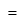 | 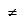 | 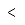 | 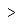 | 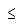 | 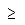 |
 | |||||
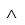 |  | ||||
 | |||||
 | 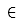 | 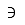 | 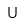 | 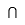 | 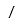 |
 | |||||
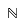 | 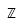 | 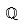 | 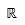 | 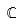 | |
 | |||||
 | |||||
 | |||||
 | |||||
 | |||||
 | |||||
 | |||||
 | |||||
 | |||||
Resolver
Sugerencia
Puedes encontrar todos los comandos disponibles relacionados con ecuaciones, inecuaciones y sistemas de ecuaciones y inecuaciones aquí.
Esta sección contiene instrucciones para encontrar soluciones de ecuaciones, inecuaciones y sistemas de ellas. Se puede hacer la acción Calc sobre ecuaciones, inecuaciones y sistemas de ellas, y se resolverán automáticamente. Alternativamente, se puede usar la instrucción solve. Los resultados serán los mismos, pero con diferente formato.
No todas las ecuaciones tienen solución en los Reales. Se puede usar resolver cen los Complejos. No a todas las ecuaciones se pueden aplicar los algoritmos para encontrar soluciones. Si el sistema no puede encontrar soluciones exactas, se puede intentar resvoler_numéricamente tpara encontrar una solución aproximada. La instrucción resolver_numéricamente no encuentra todas las soluciones; solamente encuentra una cada vez.
La acción Calc primero intenta hacer internamente el resolver completo, y si falla entonces usa resolver_numéricamente. También podemos guardar las soluciones de la ecuación en forma de conjunto y acceder a cada una de ellas utilizando los comandos descritos en el último de los siguientes ejemplos.
Nota
Escribir un sistema de ecuaciones es sencillo: separa cada ecuación por comas; escríbelas entre llaves y sepáralas por comas; o ponlas entre llaves, cada una en una nueva línea (Shift+Intro).
Resolver | |
|---|---|
 | Encuentra todas las soluciones: todos los valores que cumplen la ecuación. |
 | Encuentra un único valor aproximado que cumple la ecuación. Se usa un método iterativo, y se puede entrar el valor inicial. |
 | Resuelve inecuaciones y sistemas de ellas. |
 | Evalúa el primer parámetro (expresión) reemplazando el segundo (variable) por el tercero (valor) y haciendo las operaciones. |
Ejemplos
 |
|---|
 |
 |
 |
 |
 |
 |
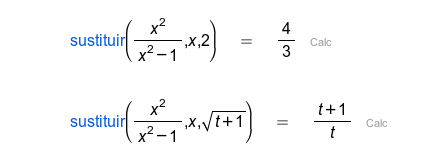 |
Griego
Es habitual usar letras griegas en las fórmulas, y en esta sección están todas. Consulta Alfabeto griego para información general.
Se pueden usar letras griegas para los nombres de las variables. Incluso se pueden usar letras chinas, japonesas o rusas, por ejemplo. Se necesita un teclado apropiado para ello, o alternativamente se pueden copiar y pegar las letras de una página web, por ejemplo. Consulta Unicode para información general.
Nota
No hay que usar este π para 3.1416; hay que usar el que está en la sección Símbolos. El π de aquí es solamente texto, no tiene valor asignado.
Lowercase | Uppercase | ||
|---|---|---|---|
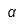 | Alfa | 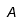 | Alfa mayúscula |
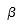 | Beta | 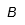 | Beta mayúscula |
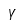 | Gamma | 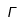 | Gamma mayúscula |
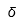 | Delta | 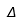 | Delta mayúscula |
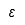 | Épsilon | 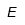 | Épsilon mayúscula |
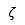 | Zeta | 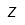 | Zeta mayúscula |
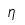 | Eta | 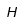 | Eta mayúscula |
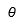 | Theta | 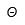 | Theta mayúscula |
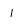 | Iota | 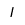 | Iota mayúscula |
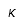 | Kappa | 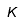 | Kappa mayúscula |
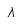 | Lambda | 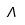 | Lambda mayúscula |
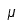 | Mu | 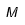 | Mu mayúscula |
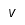 | Nu | 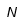 | Nu mayúscula |
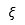 | Xi | 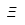 | Xi mayúscula |
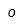 | Ómicron |  | Ómicron mayúscula |
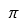 | Pi | 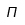 | Pi mayúscula |
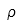 | Rho | 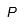 | Rho mayúscula |
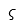 | Sigma al final | 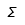 | Signa mayúscula |
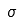 | Sigma | ||
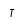 | Tau | 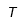 | Tau mayúscula |
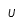 | Úpsilon | 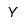 | Úpsilon mayúscula |
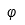 | Fi | 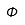 | Fi mayúscula |
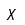 | Ji | 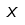 | Ji mayúscula |
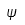 | Psi |  | Psi mayúscula |
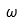 | Omega | 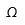 | Omega mayúscula |
Ejemplos
Griego |
|---|
 |
Unidades de medida
Sugerencia
Puedes encontrar todos los comandos disponibles relacionados con unidades de medida aquí.
Se puede calcular usando unidades. Seguimos el sistema métrico, tambien llamado Sistema Internacional de Unidades o SI. Encuentra todas las unidades y prefijos métricos soportados. Consulta Sistema métrico para información general.
Se deben escribir las unidades con los botones de esta sección. No se pueden escribir con el teclado. Una
mde aquí es unmetro, pero unamdel teclado es solamente una variable.Generalmente un espacio entre símbolos significa
producto, pero entre cantidades significa suma. Si se quiere multiplicar cantidades, se debe escribir el símbolo de multiplicar en medio.
Arriba en la sección hay un selector de prefijos del SI para las unidades de abajo. El resultado de una operación entre cantidades tiene unidades seleccionadas automáticamente. Se puede forzar la unidad de una cantidad usando la instrucción Convertir.
Instrucciones | |
|---|---|
 | Convierte la cantidad del primer parámetro en la unidad del segundo parámetro. Si no hay segundo parámetro, se convertirá a la unidad predeterminada del SI. |
 | Coeficiente de una cantidad. |
 | Unidad de una cantidad. |
Unidades
Prefijos del SI | ||
|---|---|---|
n | nano | 0.000 000 001 |
µ | micro | 0.000 001 |
m | mili | 0.001 |
c | centi | 0.01 |
d | deci | 0.1 |
da | deca | 10 |
h | hecto | 100 |
k | kilo | 1000 |
M | mega | 1 000 000 |
G | giga | 1 000 000 000 |
Unidades | ||
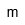 | Metro | |
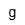 | Gramo | |
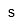 | Segundo | |
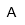 | Amperio | |
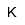 | Kelvin | |
 | Mol | |
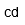 | Candela | |
 | Grado angular | |
 | Minuto angular | |
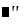 | Segundo angular | |
 | Radián | |
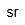 | Estereoradián | |
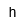 | Hora | |
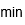 | Minuto | |
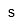 | Segundo | |
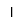 | Litro | |
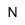 | Newton | |
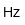 | Hertz | |
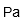 | Pascal | |
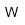 | Watt | |
 | Joule | |
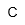 | Coulomb | |
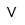 | Volt | |
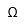 | Ohm | |
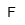 | Farad | |
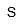 | Siemens | |
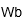 | Weber | |
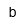 | Bar | |
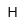 | Henry | |
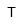 | Tesla | |
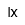 | Lux | |
 | Lumen | |
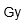 | Gray | |
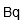 | Becquerel | |
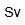 | Sievert | |
 | Katal | |
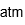 | Atmósfera | |
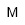 | Molar | |
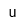 | Dalton | |
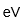 | Electronvoltio | |
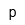 | Pondio | |
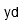 | Yard a | |
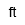 | Pie | |
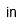 | Pulgada | |
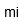 | Milla | |
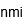 | Milla náutica | |
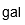 | Galón | |
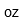 | Onza | |
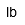 | Libra | |
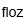 | Onza líquida | |
 | Pinta | |
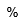 | Porciento | |
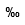 | Pormil | |
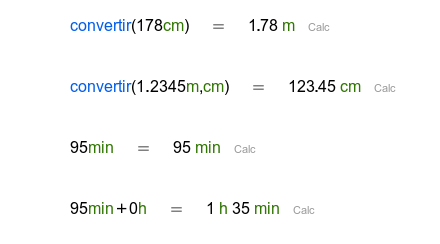
Ejemplos
Unidades de medida |
|---|
 |
 |
 |
 |
 |
 |
 |
Divisas
Además de unidades, podemos usar divisas y realizar aritmética básica con ellas, aunque no es posible convertir una divisa a otra. Debemos usar el símbolo de la divisa proporcionado en la pestaña.
Divisas | |
|---|---|
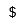 | Dólar |
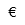 | Euro |
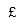 | Libra |
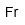 | Franco |
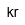 | Corona |
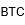 | Bitcoin |
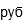 | Rublo |
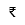 | Rupia |
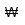 | Won |
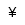 | Yen |
Example
Divisas |
|---|
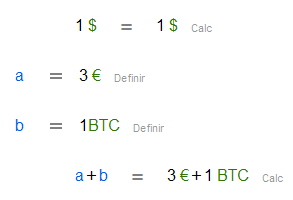 |
Gráficas
Sugerencia
Puedes encontrar todos los comandos disponibles relacionados con gráficos aquí.
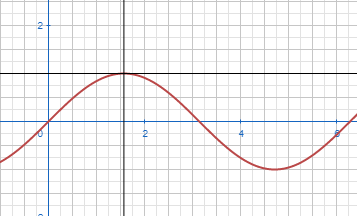
La Hoja puede tener un área para tableros, a la derecha. Los tableros son contenedores de gráficas de funciones que pueden ser configurados de muchas maneras. Tienen fondo, ejes and malla. También tienen centro y escala del punto de vista. Cada tablero tiene un nombre arriba y también un botón para configurar sus propiedades. Se puede cambiar el punto de vista en directo, arrastrando el ratón (mantener el clic mientras se mueve), o moviendo la rueda del ratón, sobre el tablero.
Hay también versiones a pantalla completa de los tableros, a las que puedes acceder haciendo clic en la flecha de abajo a la izquierda. Además, la versión grande del tablero 2-D tiene un punto de mira, y muestra abajo a la derecha las coordenadas del punto seleccionado. Esto es útil para obtener información de las funciones dibujadas.
 |
|---|
Se pueden poner gráficas en el tablero usando la acción Dibujar sobre una fórmula. Si no hay ningún tablero en la hoja, se creará uno nuevo. Sino, la gráfica se colocará en un tablero ya existente.
You can put things in the plotter by using the Plot action over a formula. If there is no plotter in the sheet, a new one will be created. Otherwise, the graph object will be placed in an existing plotter. Graph objects can also be heavily configured. Each graph object has label, color and width, and maybe border, interior and transparency. These properties can be configured by clicking the Plot action icon located next to the formula. You can also move one graph object from one plotter to another through the configuration popup next to the Plot icon.
Además, puedes crear varios objetos utilizando las acciones presentes en la barra superior o dibujándolos a mano gracias al reconocimiento de geometría manuscrito. Podrás configurarlos del mismo modo que si los hubieses creado desde la hoja. Ver Gráfica para información general.
Gráficos | |
|---|---|
Acciones | |
 | Dibujar |
 | Dibujar 3-D |
Instrucciones | |
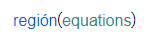 | Se ponen las fronteras en los parámetros, y se obtiene un objeto región preparado para dibujar. |
2-D
Se pueden dibujar en el plano cartesiano:
funciones, de una variable
ecuaciones, de dos variables, que son funciones implícitas
inecuaciones, de dos variables, que son regiones
listas de ellos
regiones, definidas con la instrucción
region()
Sugerencia
Se pueden dibujar elementos de EDOs, como se explica en la sección de Cálculo.
3-D
En el espacio cartesiano se pueden dibujar:
funciones, de dos variables
ecuaciones lineales, de tres variables, que son planos
listas de ellos
Ajustes del tablero
Se pueden cambiar algunos atributos del tablero haciendo clic sobre el botón de configuración en la parte superior derecha de la barra superior del tablero. Las opciones que puedes modificar son las siguientes:
Dimensiones |
|---|
 |
Color |
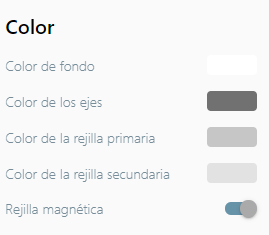 |
Horizontal |
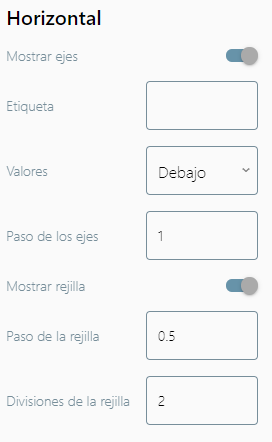 |
Vertical |
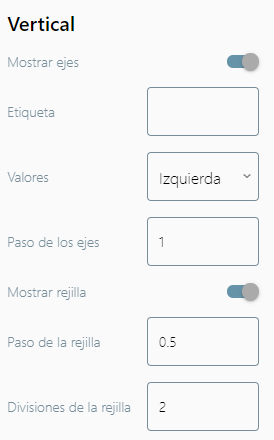 |
Todos estos atributos también pueden ser modificados desde la hoja. El comando atributos() te permite verlos así como la notación que debes utilizar para cambiar los valores por defecto.
All these settings can also be changed through the sheet. The attributes() command will allow you to see them and the notation you have to use to modify the default values.
Atributos |
|---|
 |
De este modo, podrás crear tableros como el que verás a continuación definiendo sus atributos desde la hoja.
Thus, you will be able to create plotters as the following defining their attributes by hand.
Ejemplo | |
|---|---|
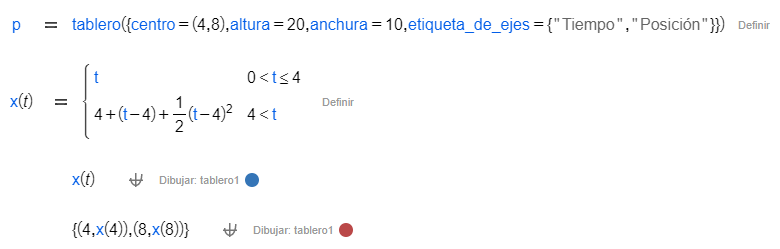 | 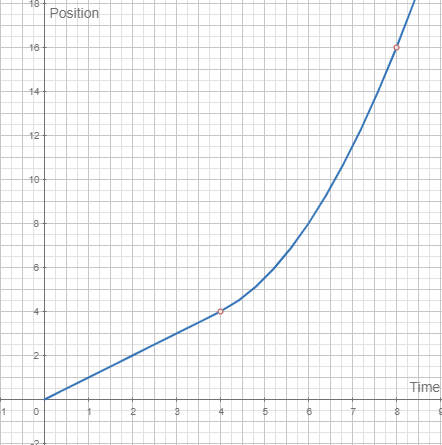 |
Conversely, for 3D plotters, you will need to use the attributes3d() command to get the associated details.
Attributes 3D |
|---|
 |
Thus, you will be able to create plotters as the following defining their attributes by hand.
Example | |
|---|---|
 |  |
Ajustes del dibujo
Tambien es posible modificar la configuración de un dibujo en particular haciendo clic sobre la representación gráfica del objecto en el tablero. Las opciones que puedes modificar son las siguientes:
Configuración del dibujo |
|---|
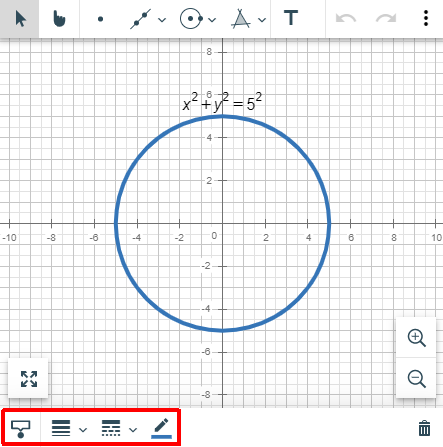 |
Las opciones que puedes modificar (de izquierda a derecha) son las siguientes:
The options you can modify (from left to right) are the following:
Fijar la etiqueta: escoge si la etiqueta del objeto es fija o no.
Grosor de línea: define el grosor de la línea.
Estilo de línea: define el estilo de la línea (sólido, rayas, puntos o rayas y puntos).
Color de línea: define el color de la línea.
Borrar: elimina el objeto dibujado.
Finalmente, también puedes cambiar la localización de una representación concreta de un tablero a otro. Para ello, debes hacer clic en el icono de la acción dibujar presente al lado del objeto representado y aparecerá en pantalla una ventana emergente como la siguiente.
Localización del dibujo |
|---|
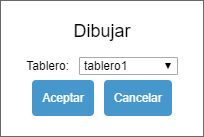 |
Nota
A partir de este momento, es posible descargar el tablero gráfico como una imagen cuadrada en formato PNG del tamaño deseado. Aprovecha esta nueva capacidad de CalcMe para guardar las imágenes generades directamente en tu dispositivo.
 |
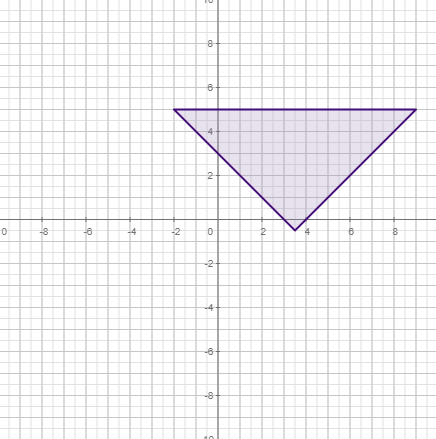
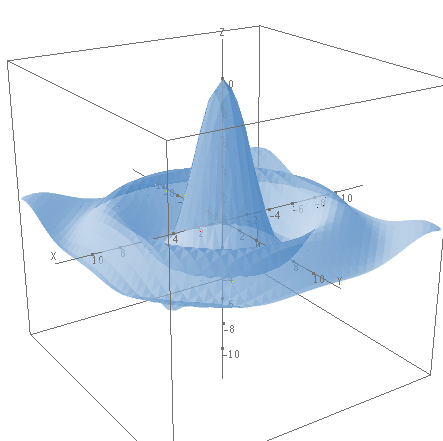
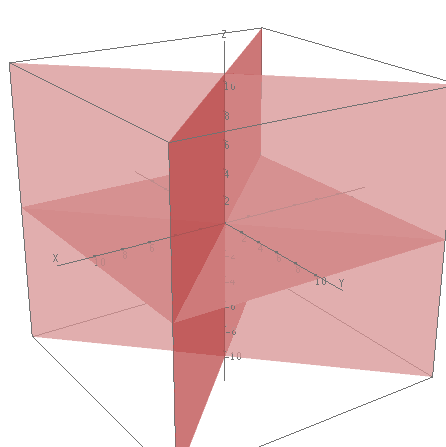
Graph
Un objeto en CalcMe se dibuja en Graph; pero Graph es mucho más que un simple visor, podemos construir segmentos, vectores, líneas y cónicas. Además, el reconocimiento de geometría manuscrito nos permite dibujar a mano, como haríamos sobre papel, y traducirá nuestros dibujos a objetos matemáticos.
 |
Sugerencia
Para más detalles, echa un vistazo a la página dedicada.
Ejemplos
 | |||||
|---|---|---|---|---|---|
 | |||||
 |  |  | |||
 | |||||
 | |||||
 |  | ||||
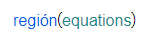 | |||||
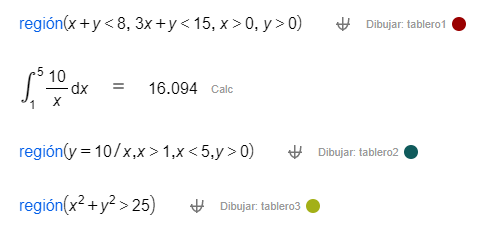 | |||||
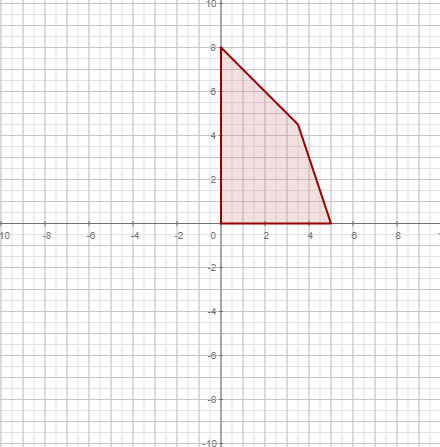 | 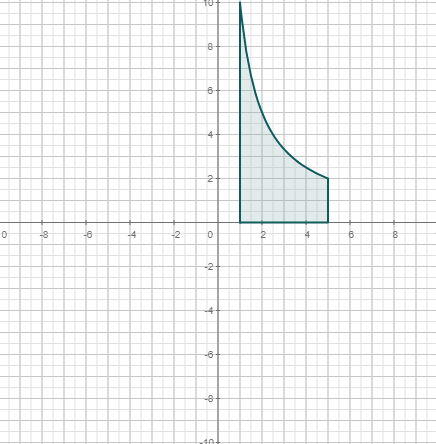 | 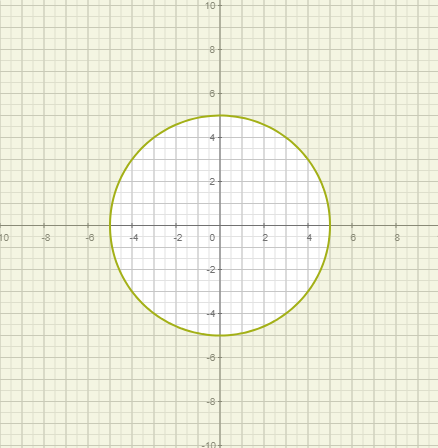 | |||
 | |||||
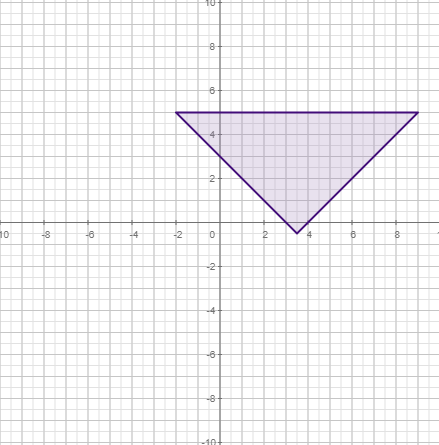 |  | 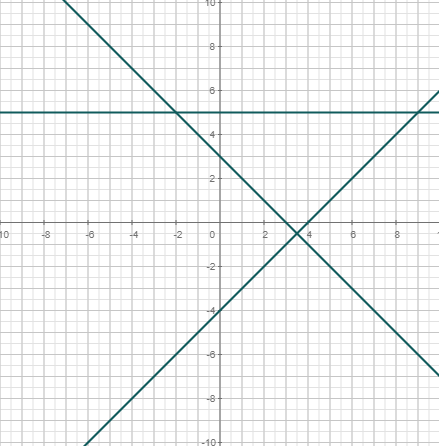 | |||
Programación
Sugerencia
Puedes encontrar todos los comandos disponibles relacionados con métodos de programación aquí.
Aquí encontrarás los comandos de programación. Éstos incluyen condicionales, bucles, bloque de inicio-fin, variables locales y devolver.
Nota
Puesto que probablemente uses los comandos explicados a continuación para generar el algoritmo de una pregunta de WirisQuizzes, en la siguiente sección se muestra como hacerlo usando la hoja y el editor de código. Puedes ver más detalles al respecto aquí.
Notación de rango
Puedes crear un rango de número usando la sintaxis: inicio..final o inicio..final..paso. It is also possible to couple ranges.También es posible juntar rangos.
Hoja de CalcMe | Editor de código de CalcMe |
|---|---|
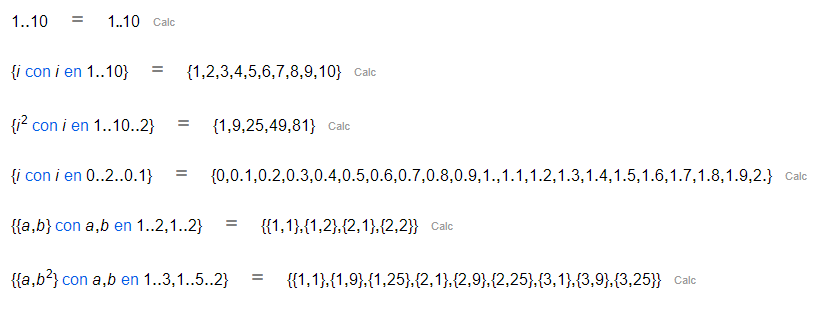 | 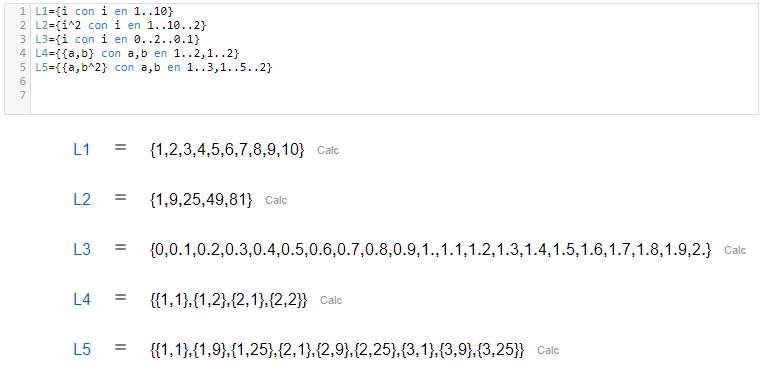 |
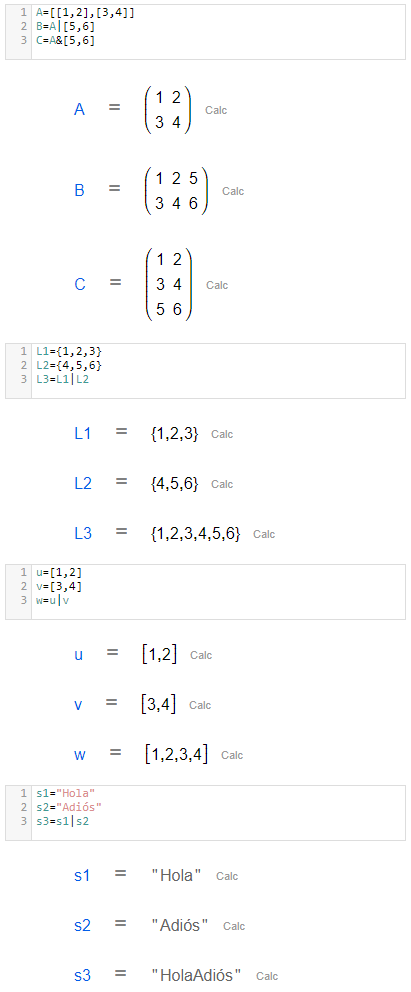
Concatenación
Podemos concatenar dos strings, listas o vectores. Además, podemos añadir una columna o una fila a una matriz fácilmente.
Hoja de CalcMe | Editor de código de CalcMe |
|---|---|
 |  |
Condicionales
Condicionales | |
|---|---|
 | Comando |
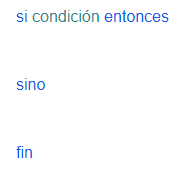 | Comando |
 | Necesita ser precedido por un |
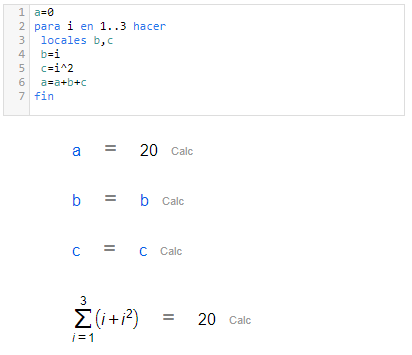
Bucles
Bucles | |
|---|---|
 | Comando |
 | Comando |
 | Comando |
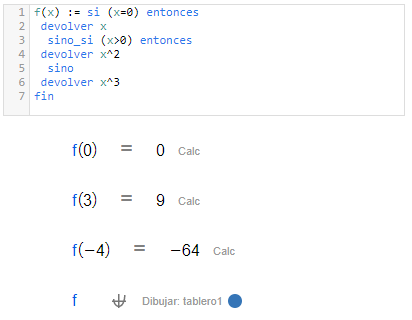
Inicio, locales y devolver
Inicio, locales y devolver | |
|---|---|
 | Este bloque es extremadamente útil cuando definimos nuestras propias funciones. Permite ejecutar varios comandos en un mismo bloque y definir variables locales. |
 | Comando |
 | Permite definir variables locales: variables definidas sólo en un bloque de código. |
Ejemplos
 | |
|---|---|
Hoja de CalcMe | Editor de código de CalcMe |
 | 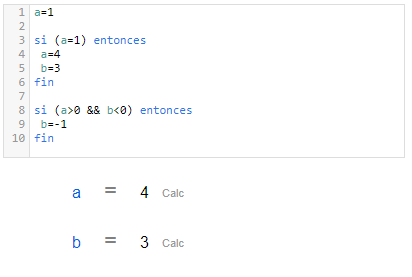 |
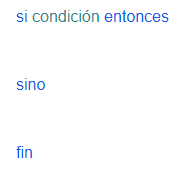 | |
Hoja de CalcMe | Editor de código de CalcMe |
 | 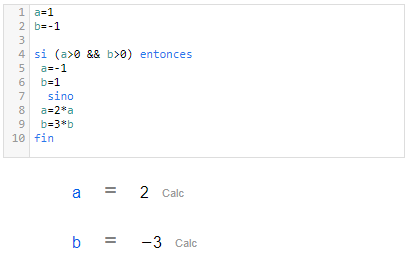 |
 | |
Hoja de CalcMe | Editor de código de CalcMe |
 | 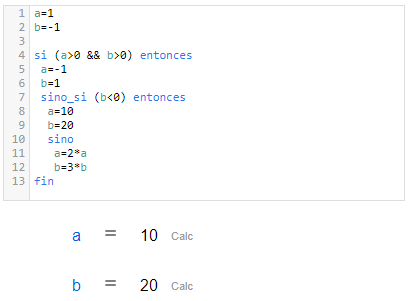 |
 | |
Hoja de CalcMe | Editor de código de CalcMe |
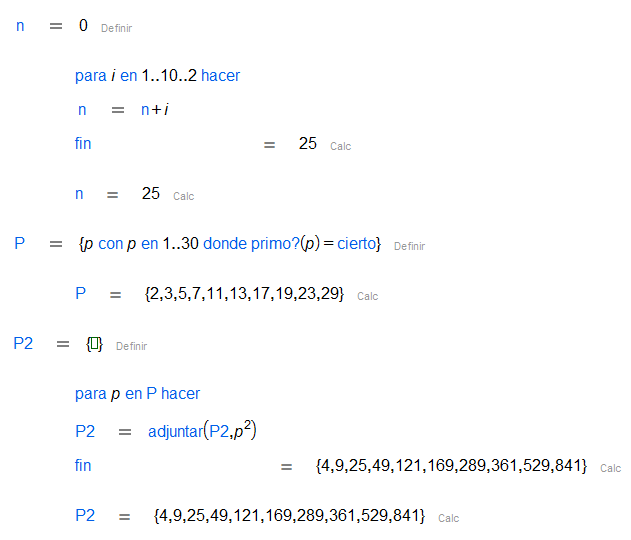 | 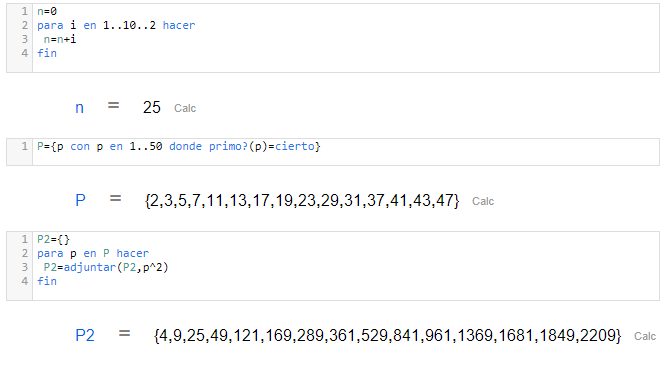 |
 | |
Hoja de CalcMe | Editor de código de CalcMe |
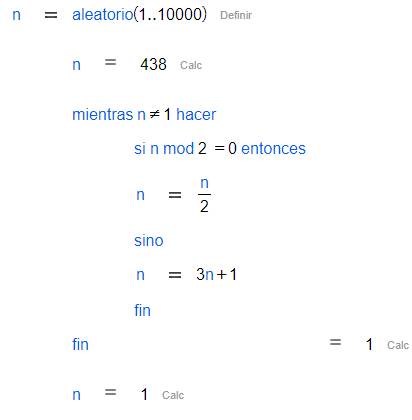 | 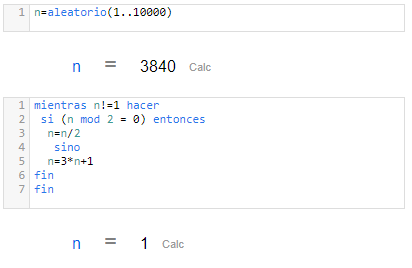 |
 | |
Hoja de CalcMe | Editor de código de CalcMe |
 | 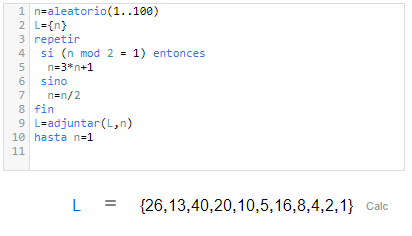 |
 | |
Hoja de CalcMe | Editor de código de CalcMe |
 |  |
 | |
Hoja de CalcMe | Editor de código de CalcMe |
  |   |
 | |
Hoja de CalcMe | Editor de código de CalcMe |
 |  |
Formato
Se pueden aplicar algunas opciones de formato pero solamente en las líneas de texto (creadas con la acción texto).
Opciones |
|---|
aplicar a letras |
Negrita (Bold) |
Cursiva (Italics) |
Color |
aplicar a la línea entera |
Fuente |
Tamaño |
Formato |
 |