Point

point(Real, Real)

point(Real, Real, Real)

point()

point(Complex)

point(Vector | List)

point(Real)

point(Line)

point(Line, Real)

point(Segment, Real)

point(Triangle)

point(Triangle, Real)

point(Circumference)

point(Ellipse | Parabola | Hyperbola, Real)

point(Polygonal | Polygon)

point(Polygonal | Polygon, Real)

point(Arc, Real)

point(Curve | Polar_curve, Real)

Constructs a point with coordinates the given numbers.

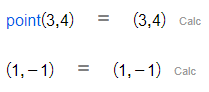Constructs a point with coordinates the given numbers.

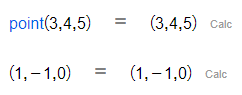Constructs the point $(0,0)$.

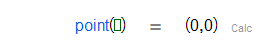Given a complex number in binomial form, constructs a point with coordinates real and imaginary part.

Given a vector or a list with two or three elements, reals, constructs a point with such coordinates.

Given a real number $x$, constructs the point $(x,0)$.

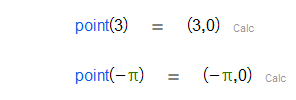Returns a point of the given line.

Given a line $y\left(x\right)$ and real number $x_0$, returns the point $y\left(x_0\right)$.

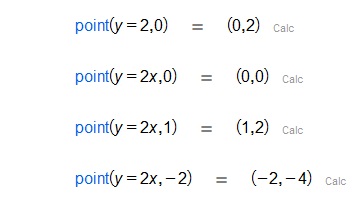Given a segment $\overline{PQ}$ and a real number $\lambda$, returns the point $\lambda \overrightarrow{PQ}$.

Returns a point of the triangle.

Returns a specific point of the triangle determined by the real number.

Returns a point of the circumference.

Given a circumference $(x-x_0{)}^2+(y-y_0{)}^2=r^2$ and a real number $\alpha$, returns the point $(x_0+r\cos \alpha ,y_0+r\sin \alpha )$.

Returns a specific point of the ellipse/parabola/hyperbola determined by the real number.

Returns a point of the polygonal or polygon.

Returns a specific point of the polygonal or polygon.

Returns a specific point given by the real number (the angle) of an arc.

Given a real number $x_0$ and a curve $f\left(x\right)$, returns a point with coordinates $(x_0,f(x_0\left)\right)$ in 2D, or $\left(f_1\right(x_0),f_2(x_0\left)\right)$ in 3D.

First vertex, Line, Plane