Partial fractions

partial_fractions(Fraction)

partial_fractions(Fraction, Ring)

Given a fraction of polynomials, returns a list $L$ whose elements are lists $L_1$, ..., $L_k$. The list $L_j$ has as elements the polynomials $f_j\left(x\right)$ and $g_j(x)$.

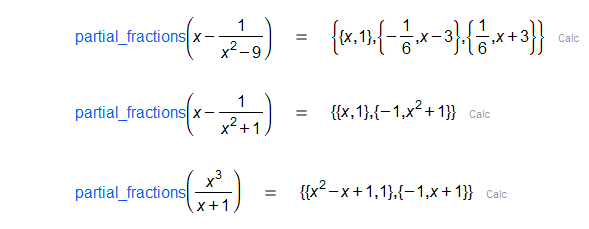Given a fraction of polynomials and a ring, returns a list $L$ whose elements are lists $L_1$, ..., $L_k$. The list $L_j$ has as elements the polynomials $f_j(x)$ and $g_j(x)$. The decomposition is done over the specified ring.

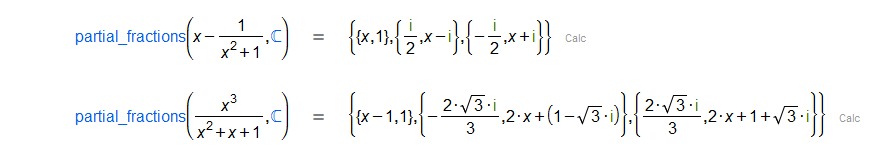Factor, Quotient and remainder