Instruccions matemàtiques bàsiques
Representació gràfica d'una funció
A l'hora de crear la gràfica d'una funció, només has d'escriure l'expressió de la funció que vols representar i fer clic sobre l'acció Dibuixa. També pots utilitzar la drecera de teclat Ctrl + Shift + P.
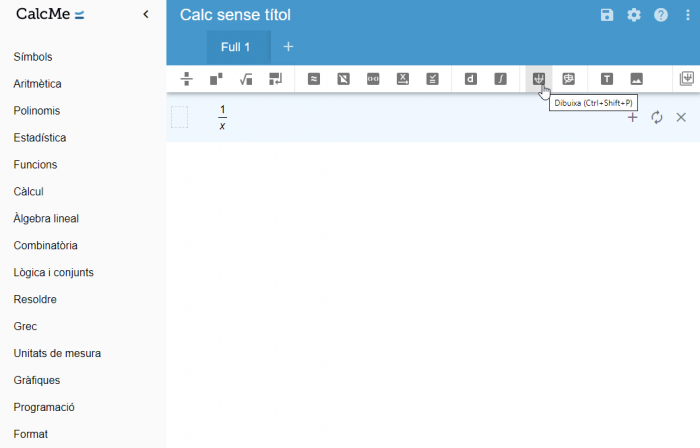
A continuació, s'obrirà un tauler amb la funció representada a la dreta de la pantalla. Per defecte, l'aparença tant de la gràfica com la del tauler segueix un estil predeterminat.
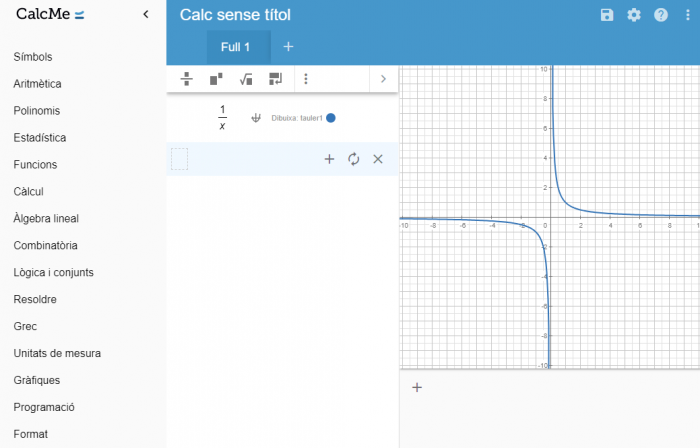
Si vols modificar algunes de les opcions d'aparença, ho pots fer definint inicialment un tauler amb les propietats desitjades. Per exemple, pots modificar-ne el centre, l'amplada, l'altura i la visibilitat de la malla utilitzant les comandes indicades.
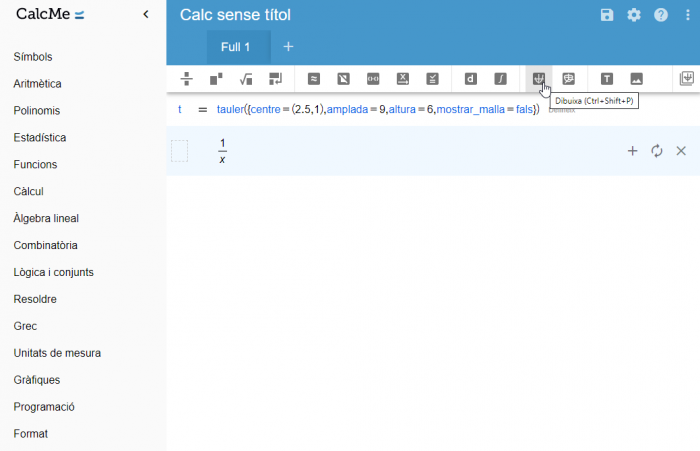
Introduint aquestes modificacions, l'aspecte del gràfic canvia completament i pot ser adaptat a les teves necessitats.
 | 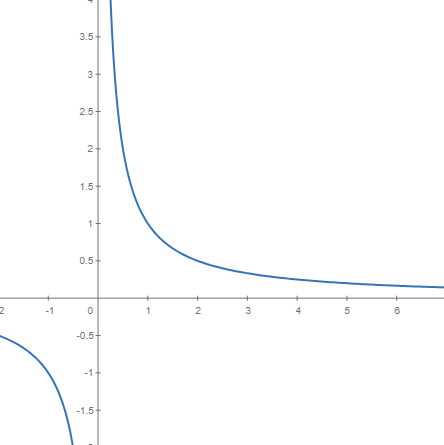 |
Suggeriment
Si vols més detalls sobre les opcions que tens a l'hora de modificar l'aparença dels gràfics, fes un cop d'ull a la seva pàgina dedicada.
Representació gràfica d'un conjunt de funcions
De la mateixa manera que amb una funció, és possible representar un conjunt de funcions en el mateix tauler. Simplement has d'escriure cada funció en una línia diferent i realitzar l'acció pertinent.
 | 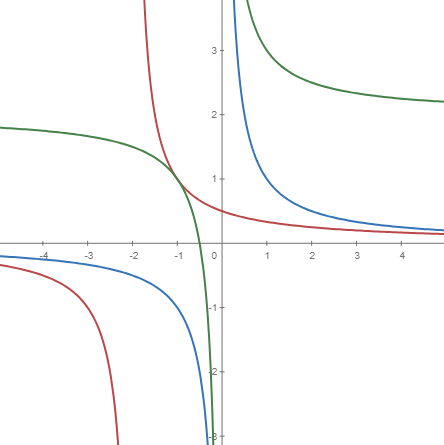 |
Per tal de distingir, més enllà de pel color, a quina funció correspon cada representació, pots fixar la seva etiqueta per tal que aparegui permanentment.
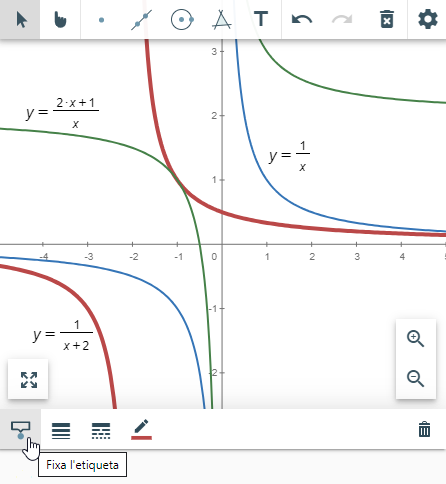
De fet, també pots canviar-ne el color, el gruix i l'estil de línia mitjançant els botons que hi ha just al cantó. Prova-ho i veuràs totes les opcions existents!
Límits
A l'hora de calcular límits, existeixen principalment dues maneres de fer-ho. Mitjançant la funció limit o a partir de la icona que pots trobar a la secció Càlcul del Menú, essent aquesta segona opció bastant més habitual.
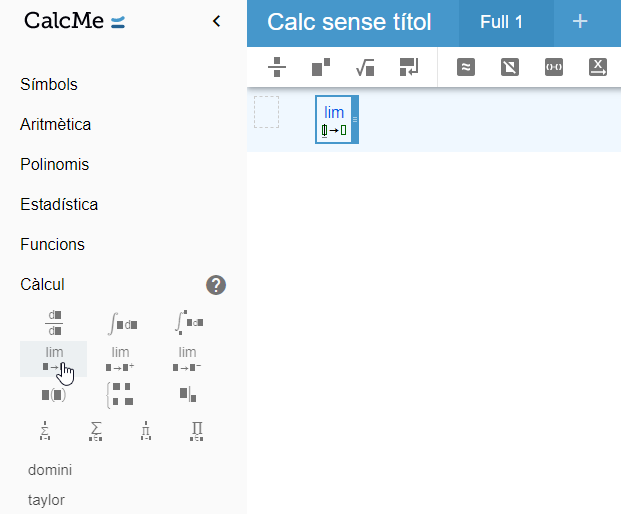
De fet, d'aquesta manera, podràs introduir fàcilment límits i límits laterals (tant per la dreta com per l'esquerra) i només hauràs d'indicar la funció i el punt en qüestió. Tingues en compte que si vols calcular límits en l'infinit, hauràs d'introduir-lo mitjançant la icona que pots trobar a la secció Símbols del Menú.
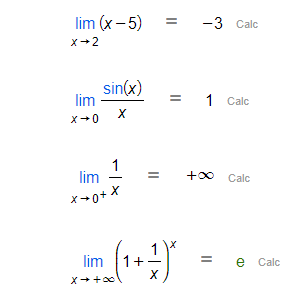 |
Aquests càlculs de límits ens poden ajudar, per exemple, a l'hora de buscar les asímptotes d'una funció. Donada la funció , volem comprovar que aquesta no té asímptotes horitzontals i que té una asímptota obliqua de la forma . Fixa't en la representació gràfica com la nostra funció s'apropa cada cop més a la seva asímptota obliqua.
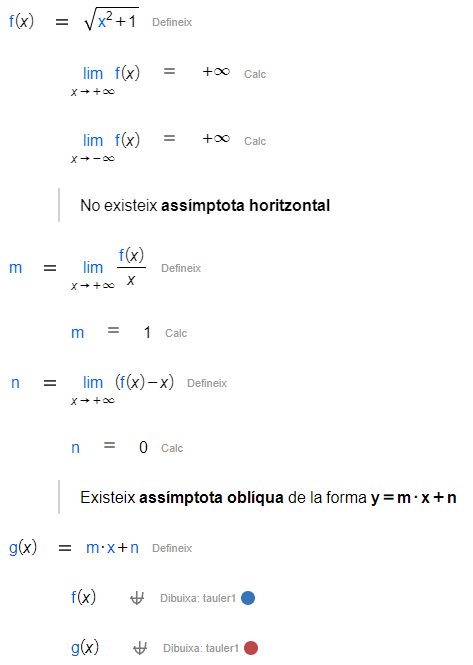 | 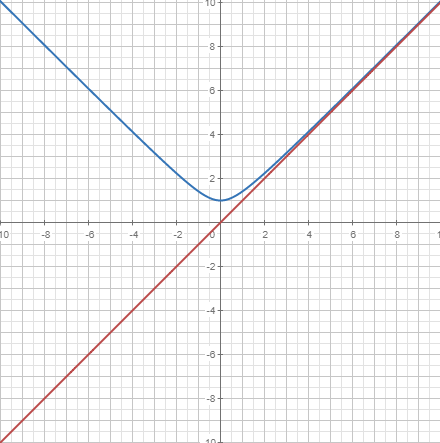 |
Suggeriment
Si vols veure com calcular límits utilitzant la mateixa funció, fes un cop d'ull a la pàgina dedicada.
Dominis
Donada una funció qualsevol, també pots obtenir fàcilment el seu domini utilitzant la comanda domini. Aquesta ens retornarà el conjunt de valors pels quals la funció està definida.
 |
De la mateixa manera, donades una funció i un punt qualsevol, pots comprovar si tal punt pertany al domini de la funció en qüestió mitjançant la comanda pertany_a_domini?. Fixa't que és necessari especificar la variable a la qual ens estem referint.
 |
Derivades
Donada una funció qualsevol, pots trobar la seva derivada de tres maneres diferents: utilitzant l'acció que pots trobar a la barra superior, mitjançant la comanda derivada, o utilitzant la icona present a la secció Càlcul del Menú. Aquesta tercera opció, plasmada a la captura de pantalla següent, és la més habitual.
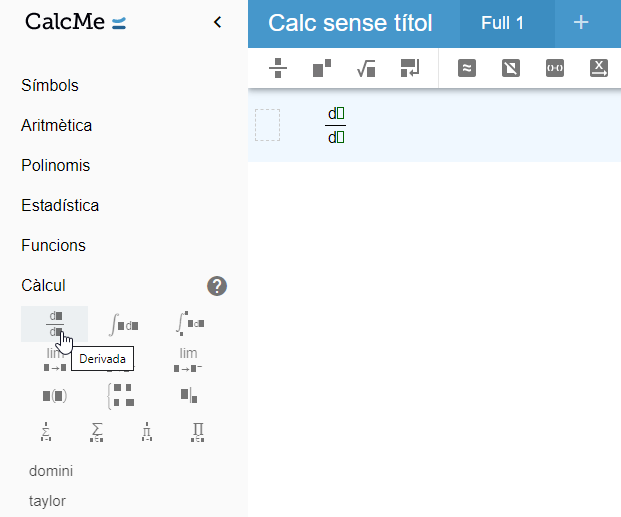
De fet, d'aquesta manera, només hauràs d'escriure la funció a derivar al numerador i la variable respecte la qual vols calcular la derivada al denominador, podent canviar-la fàcilment en cas que la funció sigui multivariant.
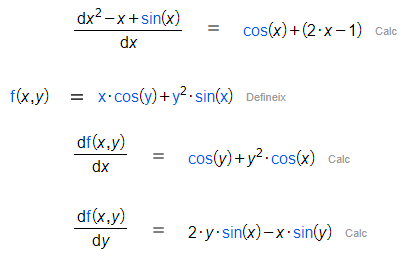 |
Per altra banda, la comanda derivada esmentada anteriorment et permet, entre d'altres, trobar directament la derivada n-èssima d'una funció.
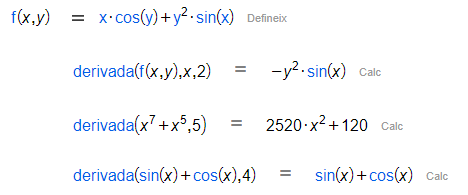 |
Suggeriment
Si vols veure la resta d'opcions per calcular derivades utilitzant la mateixa funció, fes un cop d'ull a la seva pàgina dedicada.
Integrals
De la mateixa manera que amb les derivades, donada una funció qualsevol, pots trobar la seva integral mitjançant tres procediments diferents: utilitzant l'acció que pots trobar a la barra superior, a través de la comanda integral, o utilitzant la icona present a la secció Càlcul del Menú. Aquesta tercera opció, plasmada a la captura de pantalla següent, és la més habitual.
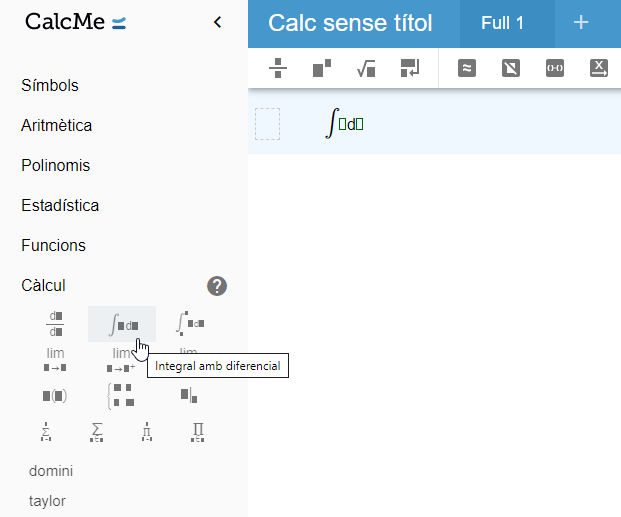
De fet, d'aquesta manera, podràs calcular integrals tant definides com indefinides només indicant la funció en qüestió i, si s'escau, l'interval d'integració. Tingues en compte que si vols calcular integrals impròpies a l'infinit, hauràs d'introduir-lo mitjançant la icona que pots trobar a la secció Símbols del Menú.
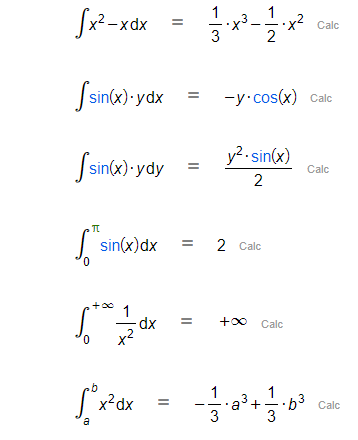 |
Per altra banda, també pots calcular integrals múltiples en concatenar integrals simples. Vés amb compte amb l'ordre en el qual escrius els diferencials, pots obtenir valors diferents!
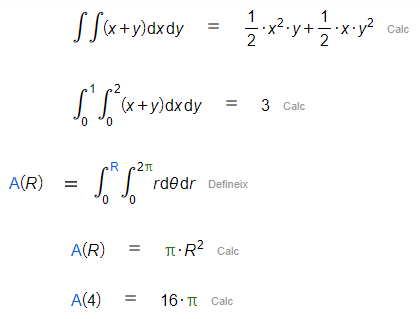 |
Suggeriment
Si vols veure com calcular integrals utilitzant la mateixa funció, fes un cop d'ull a la seva pàgina dedicada.