Interpolate
Polynomial fitting of a set of data.
Syntax
interpolate(List, List)
interpolate(List, List, Identifier)
interpolate({Point, ..., Point})
interpolate({Point, ..., Point}, Identifier)
interpolate(Relation)
interpolate(Relation, Identifier)
Description
Given two lists and , returns a polynomial of degree such that .
 |
Given two lists and and an identifier , returns a polynomial of degree such that .
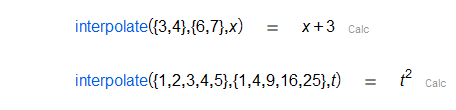 |
Given a set of points , , returns a polynomial of degree such that .
 |
Given a set of points , , and an identifier , returns a polynomial of degree such that .
 |
Given a relation , returns a polynomial of degree such that .
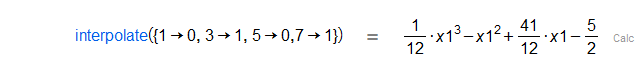 |
Given a relation and an identifier , returns a polynomial of degree such that .
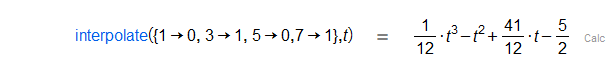 |