Legendre
Returns the Legendre symbol. Let be an odd prime. An integer is a quadratic residue modulo if it is congruent to a perfect square modulo , and is a quadratic nonresidue modulo otherwise. The Legendre symbol is a function of and defined as
Syntax
legendre(Integer, Integer)
Description
Given an integer and an odd prime , computes the Legendre symbol .
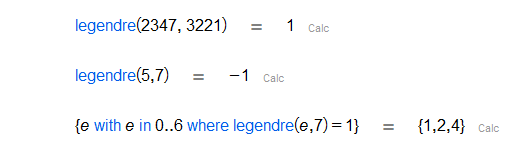 |