Ellipse
Constructs an ellipse. The equation of an ellipse with center at point with axes parallel to x- and y-axis is
Syntax
ellipse(Real, Real, Point)
ellipse(Real, Real, Vector)
ellipse(Real, Real)
ellipse(Real, Real, Point, Vector)
ellipse(Real, Real, Point, Real)
ellipse(Real, Real, Real)
Description
Given two reals and and a point , constructs an ellipse with semi-major axis , semi-minor axis and center .
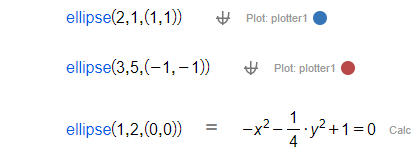 | 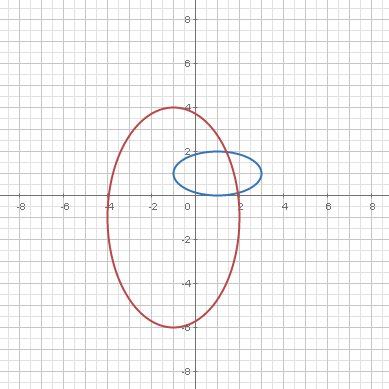 |
Given two reals and and a vector , constructs an ellipse in the direction of , with semi-major axis , semi-minor axis and center the origin.
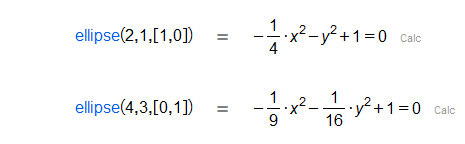 |
Given two reals and , constructs an ellipse with semi-major axis , semi-minor axis and center the origin.
 |
Given two reals and , a point and a vector , constructs an ellipse in the direction of , with semi-major axis , semi-minor axis and center .
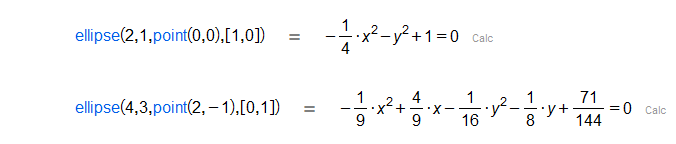 |
Given two reals and , a point and a real , constructs an ellipse in the direction given by the angle , with semi-major axis , semi-minor axis and center .
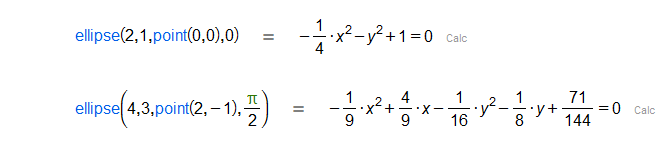 |
Given three reals , and , constructs an ellipse in the direction given by the angle , with semi-major axis , semi-minor axis and center the origin.
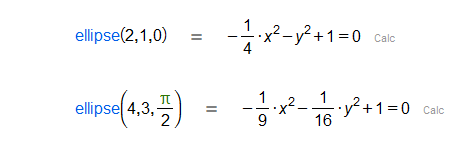 |