Instruccions d'àlgebra

Els nombres

Nombres complexos

Per definir i operar amb nombres complexos, hauràs d'introduir la unitat imaginària $i = \sqrt{- 1}$ mitjançant la icona present a la secció Symbols del Menu o utilitzant la drecera de teclat Ctrl+J. Fixa't que el nombre imaginari apareix en color verd, en cas contrari CalcMe l'interpreta com una variable qualsevol.

A partir d'aquí, pots escriure de manera natural nombres complexos en forma binòmica i trobar la seva part real i imaginària, la seva norma, el seu argument, la seva representació en forma polar, el seu conjugat i el seu invers utilitzant les diferents comandes disponibles.

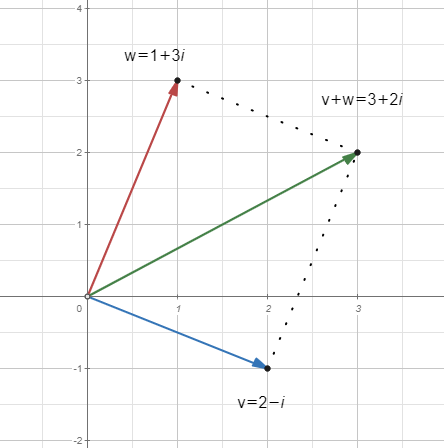
A banda, també pots operar amb aquests nombres, començant per potser les operacions més fàcils: la suma i la resta. Fixa't que sumar o restar nombres complexos acaba sent el mateix que fer-ho amb vectors del pla.

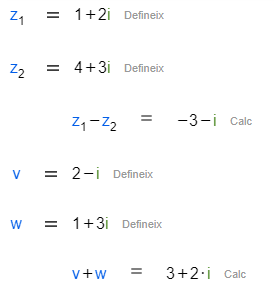En canvi, a l'hora de multiplicar dos nombres complexos $z_{1} = a + b \cdot i, z_{2} = c + d \cdot i$ , t'has d'imaginar que estàs multiplicant dos polinomis i aplicar la propietat distributiva. Com que $i \cdot i = i^{2} = - 1$ , la part real del producte serà el producte de parts reals menys el producte de parts imaginàries $a \cdot c - b \cdot d$ . mentre que la part imaginària serà la suma dels productes creuats $a \cdot d + b \cdot c$ .

Per últim, quan divideixis nombres complexos, has d'eliminar la part complexa del denominador multiplicant i dividint pel seu conjugat. D'aquesta manera, només hauràs de dividir el nombre complex del denominador per un valor real.

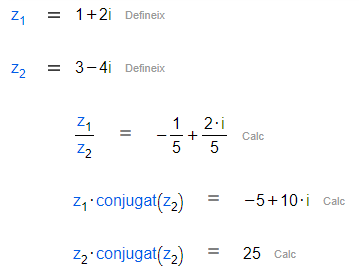Elements d'àlgebra lineal

Vectors i matrius

Per començar a treballar amb elements propis de l'àlgebra lineal, inicialment has de veure com es defineixen vectors i matrius a CalcMe. Per definir vectors, pots fer-ho de tres maneres diferents: mitjançant la comanda vector, utilitzant la icona present a la secció Àlgebra lineal del Menú, o escrivint-lo manualment. Les dues últimes són les més habituals.

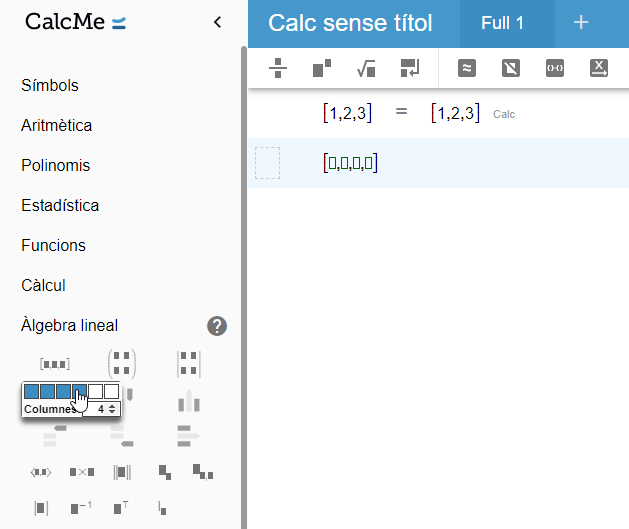
També pots definir vectors com a variables, realitzar operacions bàsiques entre ells i accedir a elements concrets d'aquests.

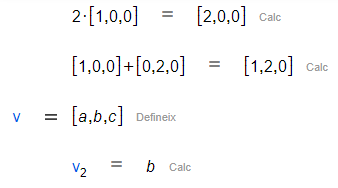Suggeriment

Si vols veure com crear vectors utilitzant la pròpia funció, fes un cop d'ull a la seva pàgina dedicada.

Per altra banda, a l'hora de definir matrius només tens dues opcions, tot i que són més que suficients. Pots utilitzar la icona que es troba al costat de la dels vectors a Àlgebra lineal o introduir-la manualment, com a vector de vectors.

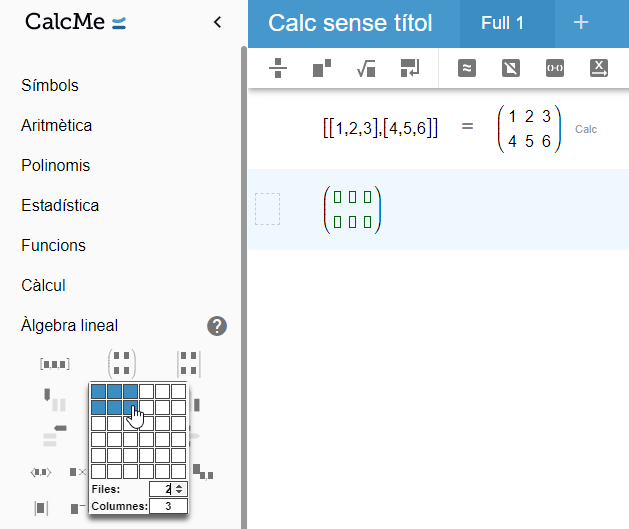
A banda, un cop creada la matriu, pots modificar-ne les dimensions inserint o eliminant files i columnes mitjançant més icones presents al Menú.

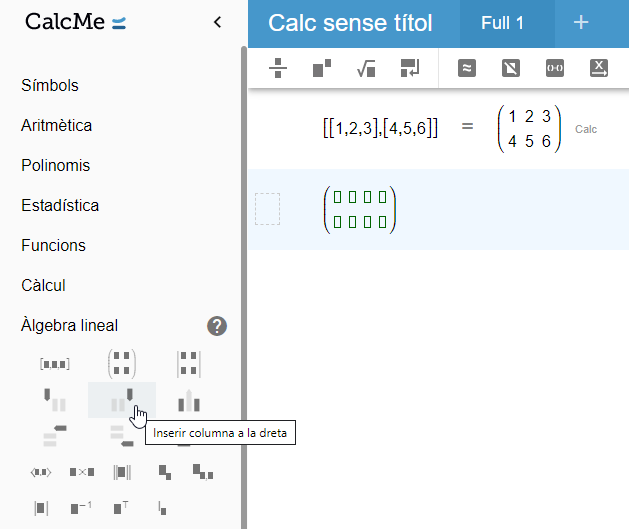
Finalment, i de la mateixa manera que amb els vectors, també pots realitzar operacions bàsiques entre matrius i accedir als seus elements.

Operacions amb matrius

A banda de les operacions bàsiques ja vistes com la suma de matrius o el producte de matrius per escalars, CalcMe et permet realitzar un gran ventall d'accions donat un conjunt de matrius. La primera de totes, el producte entre matrius.

Seguint amb operacions clàssiques amb matrius, pots també trobar comandes a la secció d'Àlgebra lineal del Menú que permeten calcular el determinant, la inversa i la transposada d'una matriu donada. De la mateixa manera, també pots crear fàcilment una matriu identitat de la dimensió que vulguis.

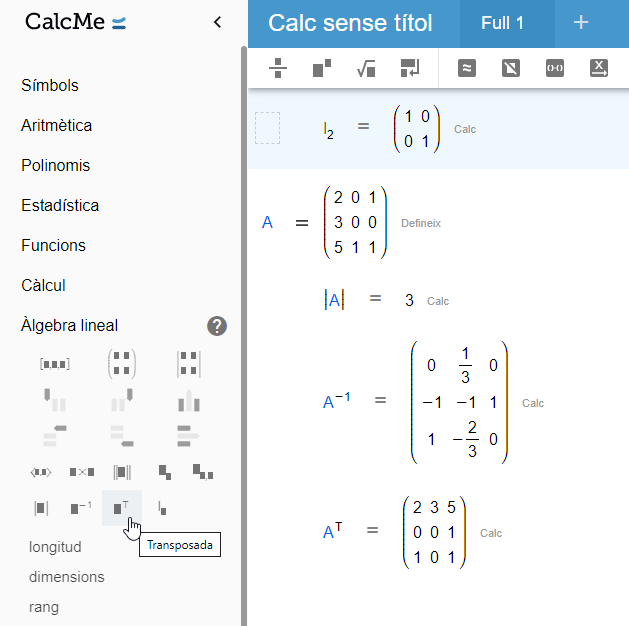
Per últim, pots trobar el rang, el nucli i la imatge d'una matriu qualsevol utilitzant les comandes corresponents.

Canvi de base

Donades dues bases d'un espai vectorial $V$ , en el nostre cas $B = {(1, 1, 1), (1, 0, 3), (3, 4, 5)}$ i $A = {(2, 3, - 1), (0, 0, 1), (2, 1, 0)}$ , la matriu $C$ que té per columnes les coordenades dels vectors de $B$ en base $A$ , s'anomena matriu del canvi de base de $B$ a $A$ . CalcMe et permet trobar aquesta matriu i, en conseqüència, les coordenades de vectors de $B$ en la base $A$ .

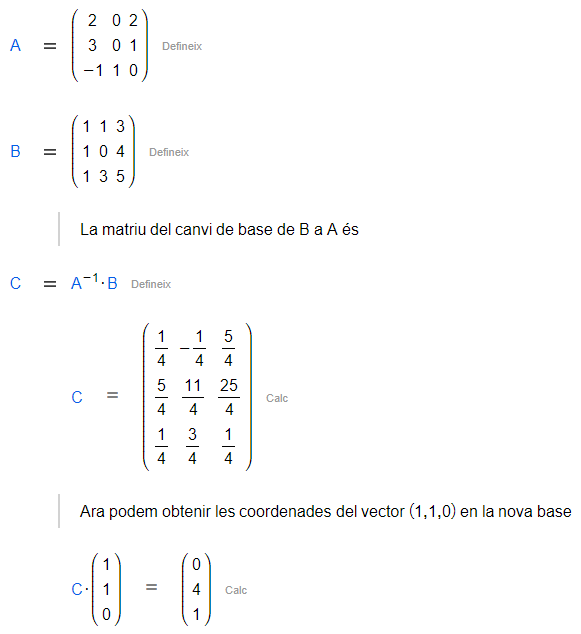Equació d'una recta al pla i a l'espai

Per crear una recta, és necessari que defineixis un punt per on ha de passar i la direcció que seguirà. Amb aquests ingredients (tot i que no són els únics possibles) i la comanda recta, pots crear i representar fàcilment una recta al pla.

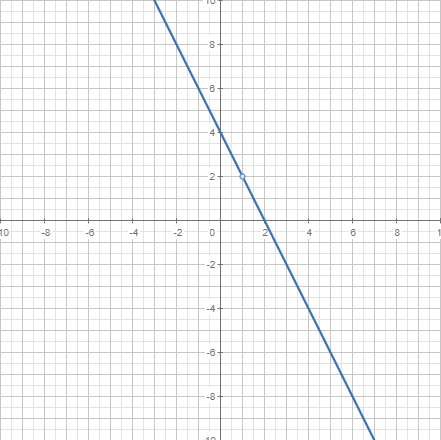Amb una sintaxi similar, pots estendre aquestes accions a l'espai i crear i representar una recta en 3 dimensions. Fixa't que la recta apareix com a intersecció de dos plans.

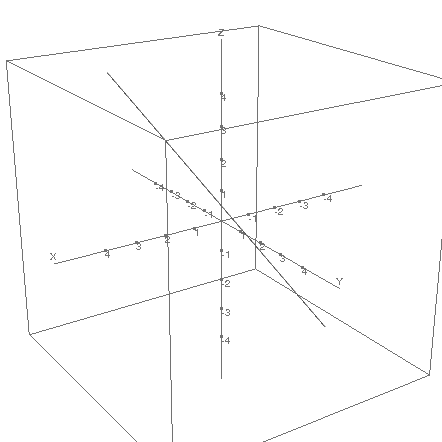Suggeriment

Si vols veure els diferents paràmetres necessaris per crear una recta, fes un cop d'ull a la seva pàgina dedicada.

Equació del pla a l'espai

Per altra banda, per crear un pla a l'espai, necessitaràs un punt i dos vectors directors. Amb aquests ingredients (tot i que no són els únics possibles) i la comanda pla, pots crear i representar fàcilment un pla a l'espai.

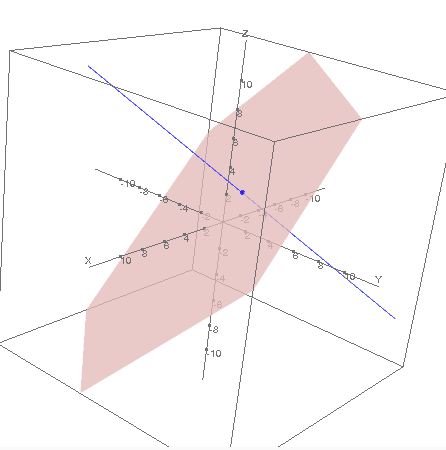
Suggeriment

Si vols veure els diferents paràmetres necessaris per crear un pla, fes un cop d'ull a la seva pàgina dedicada.

Sistemes d'equacions lineals

Solució, solució amb graus de llibertat

Per resoldre sistemes d'equacions lineals, tan determinats com amb múltiples solucions, hi ha essencialment dues metodologies: introduint les equacions manualment tot separant-les utilitzant l'acció Nova Línia (Shift + Enter) o mitjançant la comanda resol.

En cas que vulguis assignar aquestes solucions a una variable, has de tenir en compte la notació singular que s'ha d'utilitzar. A més, en el cas d'un sistema compatible indeterminat, podràs anar veient quin valor pren la solució en funció de la variable dependent.

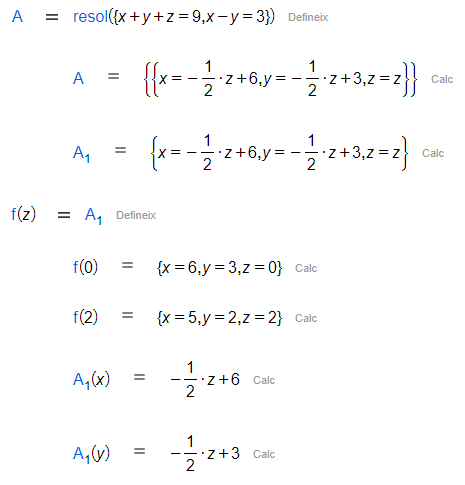La resolució de sistemes com els vists anteriorment t'obren una àmplia gamma d'opcions a l'hora de resoldre problemes amb diverses incògnites. Donat el següent esquema que mostra el flux de dades (en MB per hora) entre sis encaminadors ( $A - F$ ) d'una xarxa.

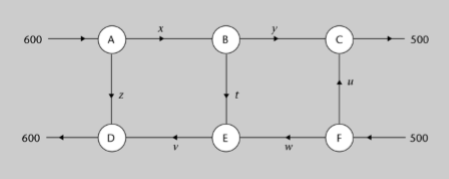Pots trobar el flux de dades entre cada parell d'encaminadors directament enllaçats ( $x, y, z, t, u, v, w$ ) si tens en compte que el flux de dades que entra per cada un d'ells és el mateix que en surt. A banda, saps que el flux total de dades entrant és de 1100 MB (per $A$ i $F$ ) i igual al flux sortint (per $C$ i $D$ ).

Afegint un parell de condicions com, per exemple, que el flux de $B$ a $C$ sigui de 200 MB per hora i que el flux de $A$ a $D$ sigui de 500 MB hora, pots trobar una única solució pel sistema d'equacions lineals.

Intersecció de plans

Tots els sistemes lineals vists anteriorment, es poden interpretar geomètricament com un conjunt de plans a l'espai que s'intersecaran en un punt (sistema compatible determinat), en una recta (sistema compatible indeterminat amb un grau de llibertat), en un pla (sistema compatible indeterminat amb dos graus de llibertat) o en cap punt (sistema incompatible).

Quan el rang de la matriu dels coeficients del pla coincideixi amb el rang de la matriu ampliada, els plans s'intersecaran en un o més punts (el conjunt de solucions del sistema lineal corresponent). A més, si aquest rang és el mateix que el nombre d'incògnites, aquesta intersecció serà un únic punt.

Per altra banda, si aquests rangs coincideixen entre si però són menors que el nombre d'incògnites, els plans s'intersecaran en un nombre infinit de punts. Si el sistema té un grau de llibertat, s'intersecaran en una recta, si en té dos, en un pla.

Aquesta situació també es pot donar en considerar més de dos plans. De fet, n'hi ha infinits que passin per una recta donada.

Per últim, si els plans són paral·lels (mateixos vectors directors però diferents punts), no existirà cap punt d'intersecció i es tractarà del cas del sistema incompatible.

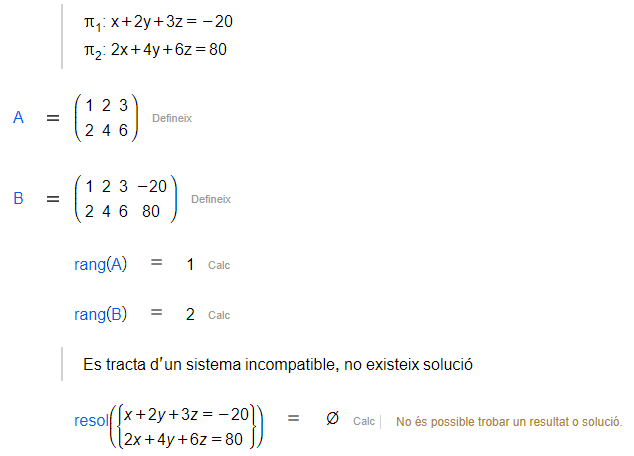De la mateixa manera, donats dos plans paral·lels, qualsevol altre pla que afegim a la situació podrà intersecar-se (o no) amb els plans inicials però mai aconseguir que el sistema tingui alguna solució.

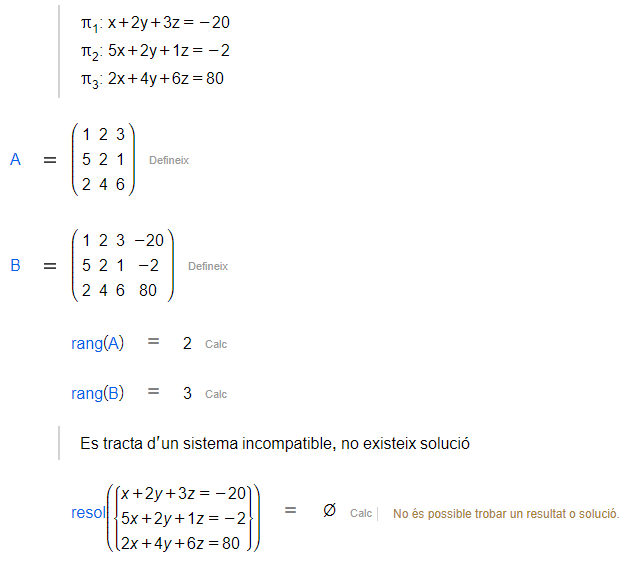Aplicacions lineals

Donat un endomorfisme $f$ qualsevol i la seva matriu $A$ , pots utilitzar les comandes imatge i nucli per trobar el conjunt de vectors que són imatge d'algun dels vectors inicials ( $I m (f)$ ) i el conjunt de vectors la imatge de $f$ pels quals és 0 ( $K e r (f)$ ).

Per altra banda, també pots trobar els valors propis i vectors propis corresponents de l'endomorfisme utilitzant les comandes vaps i veps: Com ja deus saber, es verifica que $A \cdot v_{i} = λ_{i} \cdot v_{i}$ .

De la mateixa manera, pots calcular aquests valors i vectors propis a partir del polinomi característic. Un cop calculats, pots utilitzar-ho per trobar la matriu de l'aplicació en forma diagonal a la base de vectors propis.

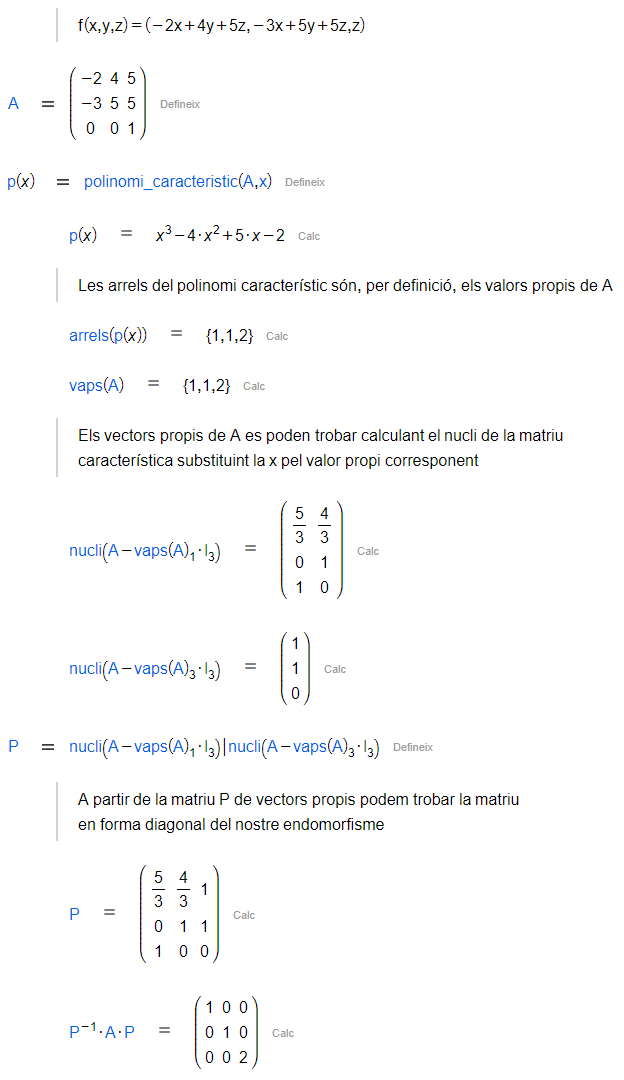Una de les aplicacions d'aquesta descomposició és trobar potències de grau elevat de la matriu inicial. Com que $A = P \cdot D \cdot P^{- 1}$ , si vols calcular $A^{n}$ només hauràs d'elevar la matriu diagonal $D$ (és a dir, els vaps) a l'enèsima potència i multiplicar per la matriu $P$ i la matriu $P^{- 1}$ .

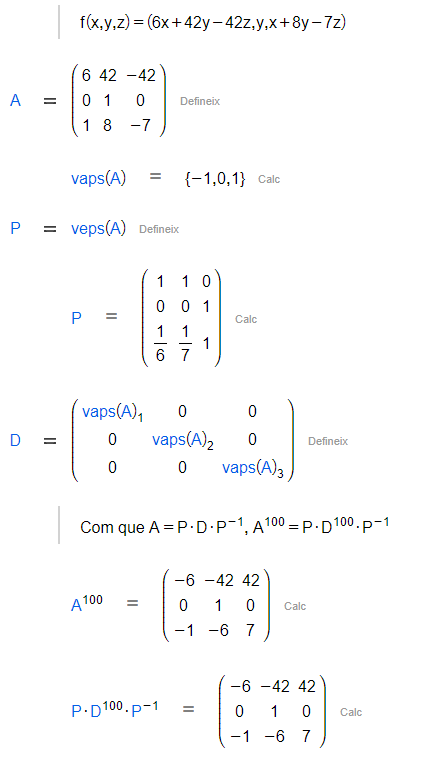Transformacions geomètriques

Translació

La translació és una transformació que mou objectes sense causar-los cap deformació, atès que cada punt de l’objecte és traslladat en la mateixa direcció i a la mateixa distància. Per tal de definir-la, només has d'establir la distància de translació (tant en l'eix $x$ com en l'eix $y$ ).

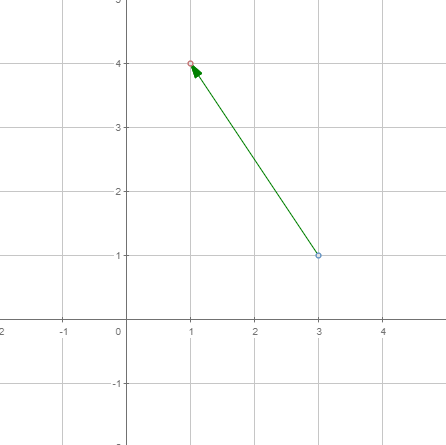De fet, pots aplicar aquesta transformació a objectes més complexos que punts.

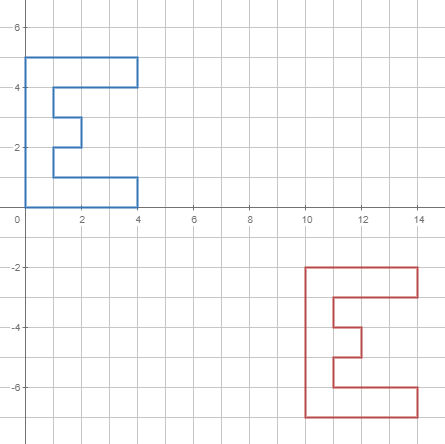Rotació

En aplicar una rotació sobre un punt $P$ , la posició d’aquest es modifica, seguint una trajectòria circular en el pla. Per tal de definir-la, has d'establir l'angle de rotació i el punt de rotació o pivot. Si no ho indiques CalcMe interpretarà que el pivot és l'origen.

Tal com has vist anteriorment, també pots aplicar aquesta transformació a un objecte més complex.

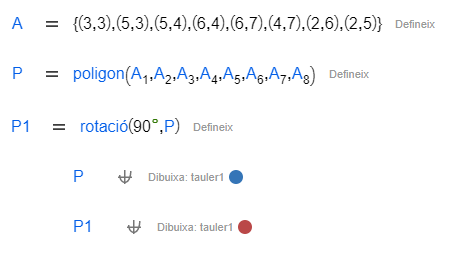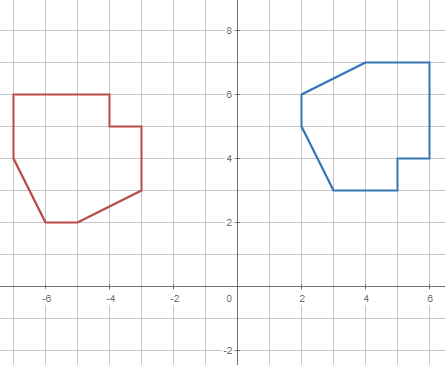O especificant un altre punt de rotació diferent de l'origen.

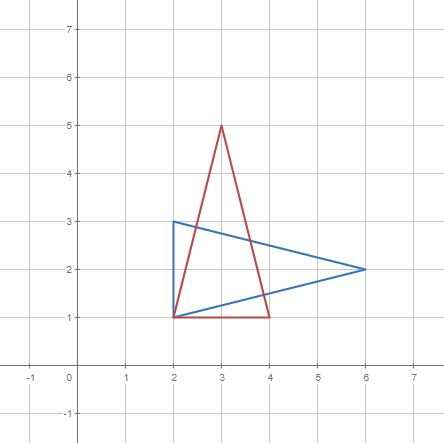Escalatge

Aplicar un escalatge sobre un punt $P$ emprant un punt fix $P_{0}$ , implica multiplicar per uns factors donats les distàncies horitzontal i vertical entre $P_{0}$ i $P$ . Si no ho indiques, CalcMe interpretarà que el punt $P_{0}$ és l'origen.

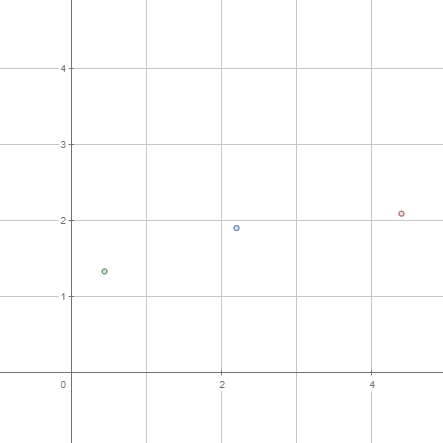Tal com has vist anteriorment, també pots aplicar aquesta transformació a un objecte més complex.

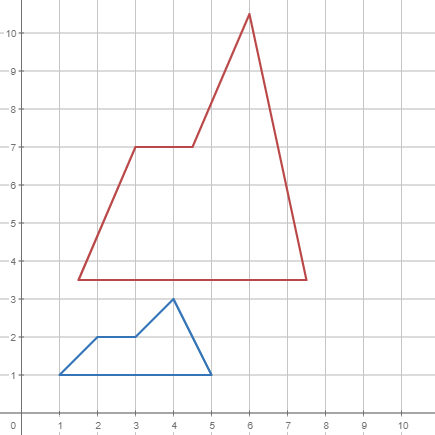O especificant un altre punt fix diferent de l'origen. En aquest cas, hauràs de començar aplicant una translació de tal manera que el punt fix coincideixi amb l'origen de coordenades. Un cop fet el moviment, has d'aplicar l'escalatge i, per acabar, desfer la translació.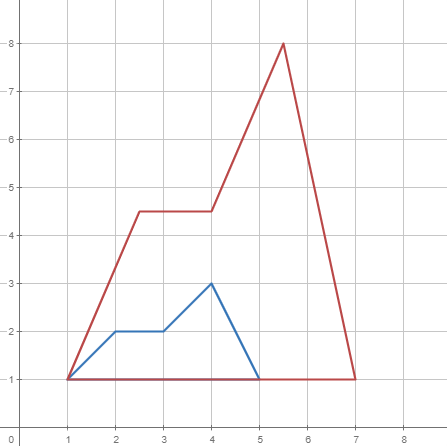